Поверхностное натяжение. Капиллярные явления

Условия, в которых находятся молекулы жидкости в объеме и непосредственно у границ раздела жидкости с газом или твердыми стенками, отличаются. Система сил оказывается неравномерной, и появляется равнодействующая, направленная внутрь или наружу объема.

Система, находящаяся в равновесии, занимает то из возможных для нее положений, которое соответствует минимуму энергии. Эти силы направлены по касательной и называются силами поверхностного натяжения. Коэффициент поверхностного натяжения можно выразить:

,

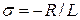где 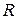– сила поверхностного натяжения,

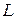– длина линии, ограничивающая поверхность раздела.

Сила поверхностного натяжения оказывает на жидкость дополнительное давление, нормальное к её поверхности, и может быть определена по формуле:

,

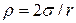где 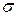– коэффициент поверхностного натяжения,

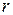– радиус трубки, в которой находится жидкость.

Размерность – СИ [Н/м], сГс – [дин/см]. Для системы вода–воздух при t= 20º С 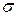=0,073 Н/м, ртуть–воздух – 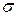=0,48 Н/м.

Силы молекулярного взаимодействия между жидкостью и твердыми стенками создают искривление свободной поверхности вблизи стенок (вогнутое или выпуклое, смачиваемое или несмачиваемое).

В результате этого уровень в капиллярах повышается или понижается. Высота капиллярного подъема (опускания) жидкости:

,

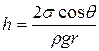где 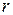– радиус трубки,

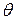– краевой угол.

При малых радиусах 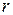подъем может быть значительным. Например, для воды высота капиллярного подъема: 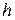= 29,8/ 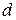, а для ртути – опускание 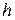= 10,15/ 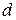, где диаметр 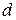принимается в мм.

Благодаря действию поверхностного натяжения объем жидкости, на который не действуют никакие другие силы, принимают сферическую форму. С этим свойством связана способность жидкости образовывать капли (рис. 3).

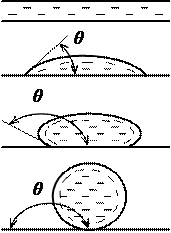Полное смачивание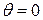

Частичное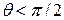

Частичное несмачивание

Полное несмачивание

Рисунок 3 – Форма капли

Давление насыщенных паров. Давлением насыщенных паров (p_н.п), или упругостью паров, называют давление, при котором пары жидкости находятся в равновесии с жидкостью и число молекул, переходящих из жидкости в пар, равно числу молекул, совершающих обратный переход. Оно в значительной степени зависит от температуры и, как правило, увеличивается с ее повышением.

Давление насыщенных паров можно определить как давление, соответствующее точке кипения жидкости при данной температуре.

Растворимость газов в жидкостях происходит при всех условиях, но различна для разных жидкостей и изменяется с увеличением давления. Она характеризуется количеством растворенного газа в единице объема жидкости.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, т. е.:

Wг/Wж = kр₂/р₁

где Wг – объем растворенного газа при нормальных условиях,

Wж – объем жидкости, k – коэффициент растворимости,

р₂ и р₁ – конечное и начальное давление газа.

При понижении давления в жидкости происходит выделение растворенного газа, причем более интенсивно, чем растворение. Это отрицательно сказывается на работе гидросистем.

Неньютоновские жидкости. Основные понятия

Неньютоновскими, или аномальными, называют жидкости, которые не подчиняются основному закону внутреннего трения Ньютона–Петрова. Они достаточно часто встречаются в природе и имеют широкое применение в быту и технике.

Основной характеристикой неньютоновских жидкостей являются так называемые кривые течения (реограммы), изображающие графически зависимость между градиентом скорости (скоростью сдвига), обозначаемым 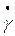, и возникающим в ней касательным напряжением .

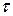Для ньютоновских жидкостей кривые течения носят линейный характер, описываются уравнением

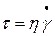или

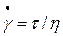
и изображаются на графике прямыми линиями, проходящими через начало координат (рис. 4). Вязкость этих жидкостей определяется углом наклона соответствующей прямой реограммы к горизонтальной оси и является единственной постоянной, полностью характеризующей реологические свойства жидкости при данных температуре и давлении независимо от градиента скорости.

.

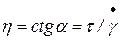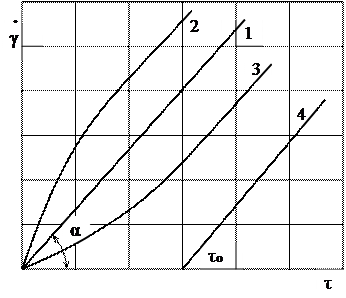Кривые течения неньютоновских жидкостей весьма многообразны и в общем случае не являются линейными. Расположение этих кривых на графике и их форма (рис. 4) определяют класс неньютоновской жидкости и характеризуют особенности ее течения.

1 – ньютоновская жидкость

2 – дилатантная жидкость

3 – псевдопластичная жидкость

4 – вязкопластичная жидкость

Рисунок 4 – Примеры реологических кривых течения жидкостей

Кривые течения псевдопластичных и дилатантных жидкостей хорошо описываются степенной зависимостью вида:

,

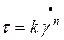где k – мера консистенции жидкости;

n – характеристика степени неньютоновского поведения жидкости;

k, n – постоянные для данной жидкости величины;

Чем выше вязкость, тем больше значение k, а чем больше значение n отличается от единицы (ньютоновская жидкость), тем сильнее проявляются её неньютоновские свойства. Для псевдопластичной жидкости n<1, а для дилатантной n>1.

Для вязкопластичной жидкости уравнение может быть записано в следующем виде:

,

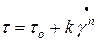где: 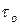– предел текучести или начальное напряжение сдвига.

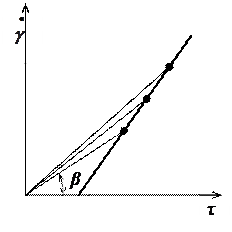
Для характеристики реологических свойств неньютоновсих жидкостей вводится понятие эффективной кажущейся вязкости. Это некоторая условная характеристика, используемая при выполнении расчетов по обычным формулам гидравлики ньютоновских жидкостей. Она даже для данной жидкости не является постоянной, а зависит от градиента скорости и напряжения сдвига и определяется на реограмме углами 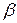наклона прямых, соединяющих начало координат с точками кривой течения.

.

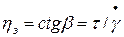Рисунок 5 – К определению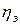

У псевдопластичных жидкостей эффективная вязкость 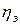с увеличением 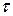или 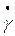уменьшается. Эти жидкости при течении как бы разжижаются. У дилатантных, наоборот, при возрастани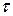и или 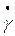вязкость 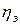увеличивается, жидкости при этом загустевают.

К неньютоновским жидкостям можно отнести многие пищевые жидкости: кефир, сметана, сгущенное молоко, томатные пасты и т. п.

ГИДРОСТАТИКА