Сходящиеся последовательности, их свойства
Определение 1. Последовательность  называется сходящейся к числу а, если последовательность
называется сходящейся к числу а, если последовательность 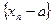 является бесконечно малой. При этом число а называют пределом последовательности
является бесконечно малой. При этом число а называют пределом последовательности  и пишут
и пишут 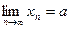 или
или 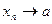 при
при 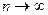 .
.
Из определения 1 следует, что любая бесконечно малая последовательность 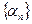 сходится к нулю, так как
сходится к нулю, так как 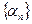 =
= 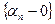 , то есть
, то есть 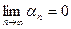 . В частности,
. В частности, 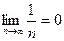 и, в силу свойств бесконечно малых последовательностей,
и, в силу свойств бесконечно малых последовательностей, 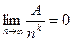 для любых
для любых 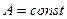 и
и 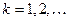 .
.
Определение 2. Последовательность  называется сходящейся к числу а, если для любого
называется сходящейся к числу а, если для любого 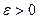 найдется номер N, такой, что
найдется номер N, такой, что 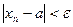 для всех значений
для всех значений 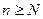 .
.
Из определения 2 получаем, что предел любой постоянной величины А равен этой постоянной величине, то есть 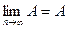 , так как для любого
, так как для любого 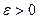
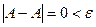 для всех значений
для всех значений 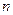 .
.
Определение 3. Последовательность  называется сходящейся к числу а, если в любой
называется сходящейся к числу а, если в любой 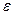 -окрестности точки а находятся все члены последовательности, начиная с некоторого номера.
-окрестности точки а находятся все члены последовательности, начиная с некоторого номера.
Определение 4. Число а называется пределом последовательности  , если для любого
, если для любого 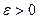 найдется номер N, такой, что
найдется номер N, такой, что 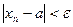 для всех значений
для всех значений 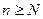 .
.
Нетрудно заметить, что определения 1-4 равносильны.
Замечание. Из определения 1 следует, что если последовательность  сходится к а, то
сходится к а, то 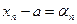 , где
, где 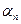 – бесконечно малая последовательность, отсюда
– бесконечно малая последовательность, отсюда 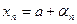 . Верно и обратное, т.е. если последовательность
. Верно и обратное, т.е. если последовательность  можно представить в виде суммы постоянной а и бесконечно малой последовательности, то последовательность
можно представить в виде суммы постоянной а и бесконечно малой последовательности, то последовательность  сходится к числу а. Действительно,
сходится к числу а. Действительно, 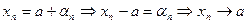 по определению 1.
по определению 1.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство. Предположим, что последовательность  имеет два предела: с и d. Тогда
имеет два предела: с и d. Тогда 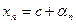 и
и 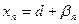 , где
, где 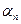 и
и 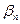 – бесконечно малые последовательности (см. замечание выше). Отсюда
– бесконечно малые последовательности (см. замечание выше). Отсюда 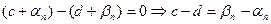 . Поскольку
. Поскольку 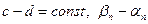 – бесконечно малая последовательность, по теореме 5 §4
– бесконечно малая последовательность, по теореме 5 §4 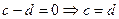 . Теорема доказана.
. Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность ограничена.
Доказательство. По определению 1 последовательность 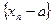 бесконечно малая, по теореме 4 §4 она ограничена, то есть существует число M > 0, такое, что
бесконечно малая, по теореме 4 §4 она ограничена, то есть существует число M > 0, такое, что 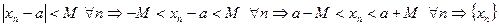 одновременно ограничена и снизу и сверху, поэтому ограничена. Теорема доказана.
одновременно ограничена и снизу и сверху, поэтому ограничена. Теорема доказана.
Теорема 3. Сумма (разность) сходящихся последовательностей есть сходящаяся последовательность, причем
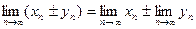 .
.
Доказательство. Пусть 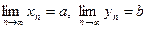 . Тогда
. Тогда 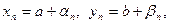
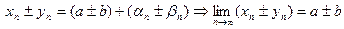 (см. замечание в начале параграфаи свойства бесконечно малых последовательностей). Теорема доказана.
(см. замечание в начале параграфаи свойства бесконечно малых последовательностей). Теорема доказана.
Теорема 4. Произведение сходящихся последовательностей есть сходящаяся последовательность, причем
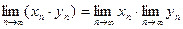 .
.
Доказательство. Имеем 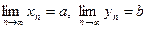 ,
, 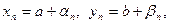
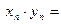
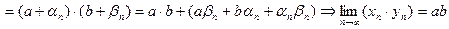 , так как
, так как 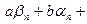
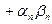 – бесконечно малая последовательность (см. замечание и свойства бесконечно малых последовательностей). Теорема доказана.
– бесконечно малая последовательность (см. замечание и свойства бесконечно малых последовательностей). Теорема доказана.
Следствие. Постоянный множитель можно выносить за знак предела, то есть 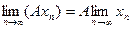 .
.
Это очевидно, так как 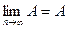 .
.
Теорема 5. Частное 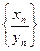 двух сходящихся последовательностей
двух сходящихся последовательностей  и
и 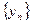 , таких, что
, таких, что 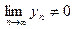 , определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, причем
, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, причем
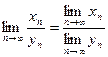 .
.
Для доказательства теоремы 5 нам потребуется вспомогательное утверждение.
Лемма. Если последовательность 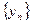 сходится к числу
сходится к числу 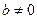 , то последовательность
, то последовательность 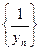 ограничена
ограничена 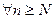 , где N – некоторое натуральное число.
, где N – некоторое натуральное число.
Доказательство. Положим 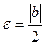 . По определению предела для него найдется номер N, такой, что для всех
. По определению предела для него найдется номер N, такой, что для всех 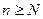 выполняется неравенство
выполняется неравенство 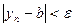 , т.е.
, т.е. 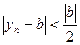 . Поскольку
. Поскольку 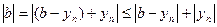 , то
, то 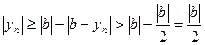 для всех
для всех 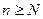 , т.е.
, т.е. 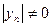 и
и 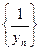 существует при
существует при 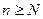 , а также
, а также 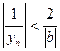 для всех
для всех 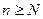 . Лемма доказана.
. Лемма доказана.
Доказательство теоремы 5. Пусть 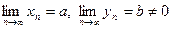 . Тогда
. Тогда 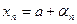 ,
, 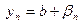 . Рассмотрим
. Рассмотрим 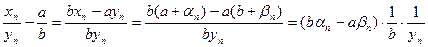 = =
= = 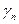 . В последнем выражении первый множитель – бесконечно малая последовательность, второй и третий – ограниченная для всех
. В последнем выражении первый множитель – бесконечно малая последовательность, второй и третий – ограниченная для всех 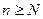 последовательность. Поэтому
последовательность. Поэтому 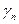 – бесконечно малая последовательность, а так как
– бесконечно малая последовательность, а так как 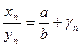 , то
, то 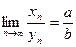 . Теорема доказана.
. Теорема доказана.
Рассмотрим теперь свойства сходящихся последовательностей, связанных знаком неравенства.
Теорема 6. Пусть  и
и 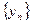 – две сходящиеся последовательности, имеющие одинаковый предел а. Если, хотя бы начиная с некоторого номера, выполнено неравенство
– две сходящиеся последовательности, имеющие одинаковый предел а. Если, хотя бы начиная с некоторого номера, выполнено неравенство
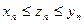 , (5.1)
, (5.1)
то последовательность 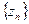 – сходящаяся, причем
– сходящаяся, причем 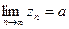 .
.
Доказательство. Пусть 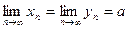 , неравенство
, неравенство 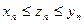 выполняется, начиная с номера
выполняется, начиная с номера 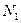 . Возьмем
. Возьмем 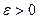 произвольно. Для него существуют
произвольно. Для него существуют 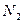 и
и 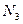 ,такие, что
,такие, что
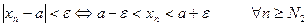 , (5.2)
, (5.2)
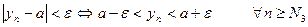 . (5.3)
. (5.3)
Положим 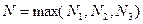 . Тогда
. Тогда 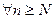 одновременно выполнены все неравенства (5.1) – (5.3), значит,
одновременно выполнены все неравенства (5.1) – (5.3), значит,
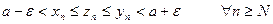 ,
,
то есть 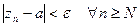 , следовательно,
, следовательно, 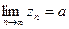 . Теорема доказана.
. Теорема доказана.
Теорема 6 часто называется «теоремой о сжатой переменной», или «теоремой о промежуточной переменной», или «теоремой о двух милиционерах». Мы ею часто будем пользоваться в дальнейшем.
Теорема 7. Если все члены двух сходящихся последовательностей  и
и 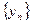 , по крайней мере, начиная с некоторого номера, удовлетворяют неравенству
, по крайней мере, начиная с некоторого номера, удовлетворяют неравенству 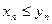 , то и пределы этих последовательностей удовлетворяют такому же неравенству, то есть
, то и пределы этих последовательностей удовлетворяют такому же неравенству, то есть 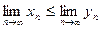 .
.
Доказательство. Пусть 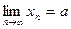 ,
, 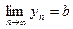 . Надо доказать, что
. Надо доказать, что 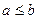 . Предположим противное, т.е. что
. Предположим противное, т.е. что 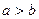 , и возьмем
, и возьмем 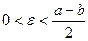 . Тогда
. Тогда 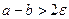 и
и 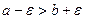 . По определению предела последовательности для этого
. По определению предела последовательности для этого 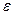 найдутся
найдутся 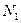 и
и 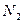 такие, что
такие, что
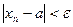 , откуда
, откуда 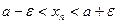 для всех
для всех 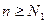 ,
,
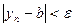 , откуда
, откуда 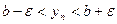 для всех
для всех 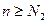 .
.
Обозначим 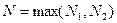 . Тогда для всех
. Тогда для всех 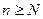 эти неравенства выполняются одновременно и, следовательно,
эти неравенства выполняются одновременно и, следовательно, 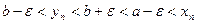 , т.е.
, т.е. 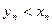 , что противоречит условию теоремы. Полученное противоречие доказывает утверждение теоремы. Теорема доказана.
, что противоречит условию теоремы. Полученное противоречие доказывает утверждение теоремы. Теорема доказана.
Следствие. Если, начиная с некоторого номера, 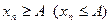 то и
то и 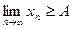 (
( 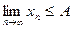 ).
).
Это очевидно, так как вместо одной из последовательностей можно рассмотреть постоянную последовательность 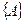 .
.
Заметим, что если 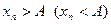 , то
, то 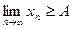 (
( 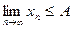 ). Например,
). Например, 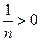 для всех n, однако
для всех n, однако 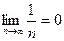 .
.
Теорема 8. Если 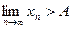 (
( 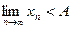 ), то, начиная с некоторого номера,
), то, начиная с некоторого номера, 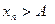
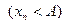 .
.
Действительно, если 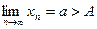 (
( 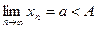 ), то, взяв окрестность точки а, не содержащую точку А, по определению 3 получим, что, начиная с некоторого номера, все члены последовательности попадут в эту окрестность, т.е. будут больше А (будут меньше А).
), то, взяв окрестность точки а, не содержащую точку А, по определению 3 получим, что, начиная с некоторого номера, все члены последовательности попадут в эту окрестность, т.е. будут больше А (будут меньше А).
§ 6. Монотонные последовательности. Число е
Определение 1. Последовательность  называется убывающей (невозрастающей), если для всех
называется убывающей (невозрастающей), если для всех 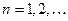 выполняется неравенство
выполняется неравенство 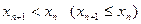 .
.
Определение 2. Последовательность  называется возрастающей (неубывающей), если для всех
называется возрастающей (неубывающей), если для всех 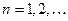 выполняется неравенство
выполняется неравенство 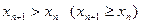 .
.
Определение 3. Убывающие, невозрастающие, возрастающие и неубывающие последовательности называются монотонными последовательностями, убывающие и возрастающие последовательности называют также строго монотонными последовательностями.
Очевидно, что неубывающая последовательность ограничена снизу, невозрастающая последовательность ограничена сверху. Поэтому всякая монотонная последовательность заведомо ограничена с одной стороны.
Пример 1. Последовательность 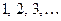 возрастает,
возрастает, 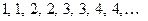 не убывает,
не убывает, 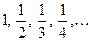 убывает,
убывает, 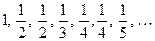 не возрастает,
не возрастает, 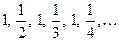 – немонотонная последовательность.
– немонотонная последовательность.
Для монотонных последовательностей важную роль играет следующая
Теорема 1. Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится.
Доказательство. Пусть последовательность  не убывает и ограничена сверху, т.е.
не убывает и ограничена сверху, т.е. 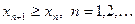 и множество
и множество  ограничено сверху. По теореме 1 § 2 существует
ограничено сверху. По теореме 1 § 2 существует 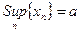 . Докажем, что
. Докажем, что 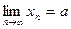 .
.
Возьмем 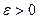 произвольно. Поскольку а – точная верхняя граница, существует номер N такой, что
произвольно. Поскольку а – точная верхняя граница, существует номер N такой, что 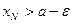 . Так как последовательность неубывающая, то для всех
. Так как последовательность неубывающая, то для всех 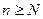 имеем
имеем 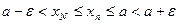 , т.е.
, т.е. 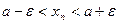 , поэтому
, поэтому 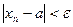 для всех
для всех 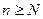 , а это и означает, что
, а это и означает, что 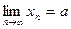 .
.
Для невозрастающей последовательности, ограниченной снизу, доказательство проводится аналогично (студенты могут доказать это утверждение дома самостоятельно). Теорема доказана.
Замечание. Теорему 1 можно сформулировать иначе.
Теорема 2. Для того чтобы монотонная последовательность сходилась, необходимо и достаточно, чтобы она была ограничена.
Достаточность установлена в теореме 1, необходимость – в теореме 2 § 5.
Условие монотонности не является необходимым для сходимости последовательности, так как сходящаяся последовательность не обязательно монотонна. Например, последовательность 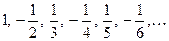 не монотонная, однако сходится к нулю.
не монотонная, однако сходится к нулю.
Следствие. Если последовательность  возрастает (убывает) и ограничена сверху (снизу), то
возрастает (убывает) и ограничена сверху (снизу), то 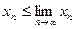 (
( 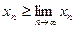 ).
).
Действительно, по теореме 1 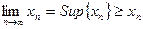 (
( 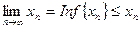 ).
).
Определение 4. Если 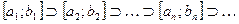 и
и 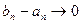 при
при 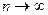 , то последовательность
, то последовательность 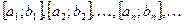 называется стягивающейся системой вложенных отрезков.
называется стягивающейся системой вложенных отрезков.
Теорема 3 (принцип вложенных отрезков). У всякой стягивающейся системы вложенных отрезков существует, и притом единственная, точка с, принадлежащая всем отрезкам этой системы.
Доказательство. Докажем, что точка с существует. Поскольку 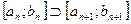 , то
, то 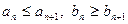 и, следовательно, последовательность
и, следовательно, последовательность 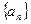 не убывает, а последовательность
не убывает, а последовательность 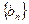 не возрастает. При этом
не возрастает. При этом 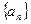 и
и 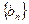 ограничены, так как
ограничены, так как 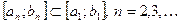 . Тогда по теореме 1 существуют
. Тогда по теореме 1 существуют 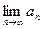 и
и 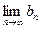 , но так как
, но так как 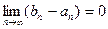 , то
, то 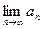 =
= 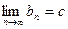 . Найденная точка с принадлежит всем отрезкам системы, так как по следствию теоремы 1
. Найденная точка с принадлежит всем отрезкам системы, так как по следствию теоремы 1 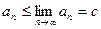 ,
, 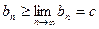 , т.е.
, т.е. 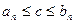 для всех значений n.
для всех значений n.
Покажем теперь, что точка с – единственная. Предположим, что таких точек две: с и d и пусть для определенности 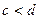 . Тогда отрезок
. Тогда отрезок 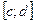 принадлежит всем отрезкам
принадлежит всем отрезкам 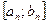 , т.е.
, т.е. 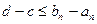 для всех n, что невозможно, так как
для всех n, что невозможно, так как 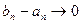 и, значит, начиная с некоторого номера,
и, значит, начиная с некоторого номера, 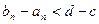 . Теорема доказана.
. Теорема доказана.
Отметим, что здесь существенно то, что рассматриваются замкнутые промежутки, т.е. отрезки. Если рассмотреть систему стягивающихся интервалов, то принцип, вообще говоря, неверен. Например, интервалы 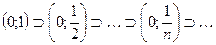 , очевидно, стягиваются в точку
, очевидно, стягиваются в точку 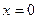 , однако точка
, однако точка 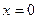 не принадлежит ни одному интервалу этой системы.
не принадлежит ни одному интервалу этой системы.
Рассмотрим теперь примеры сходящихся монотонных последовательностей.
1) Число е.
Рассмотрим теперь последовательность 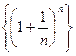 . Как она себя ведет? Основание
. Как она себя ведет? Основание
степени 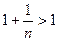 , поэтому
, поэтому 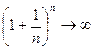 ? С другой стороны,
? С другой стороны, 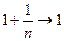 , а
, а 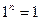 , поэтому
, поэтому 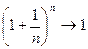 ? Или предел не существует?
? Или предел не существует?
Чтобы ответить на эти вопросы, рассмотрим вспомогательную последовательность 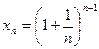 . Докажем, что она убывает и ограничена снизу. При этом нам будет нужна
. Докажем, что она убывает и ограничена снизу. При этом нам будет нужна
Лемма. Если 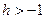 , то для всех натуральных значений n имеем
, то для всех натуральных значений n имеем
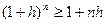
(неравенство Бернулли).
Доказательство. Воспользуемся методом математической индукции.
Если 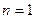 , то
, то 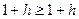 , т.е. неравенство верно.
, т.е. неравенство верно.
Предположим, что оно верно для 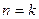 и докажем его справедливость для
и докажем его справедливость для 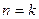 +1.
+1.
Верно 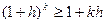 . Умножим это неравенство на
. Умножим это неравенство на 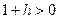 :
:
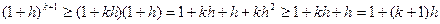 .
.
Таким образом, 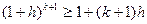 . Значит, согласно принципу математической индукции, неравенство Бернулли верно для всех натуральных значений n. Лемма доказана.
. Значит, согласно принципу математической индукции, неравенство Бернулли верно для всех натуральных значений n. Лемма доказана.
Покажем, что последовательность  убывает. Имеем
убывает. Имеем
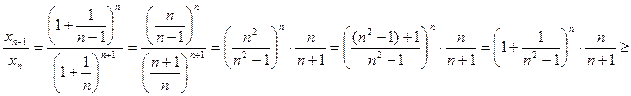
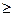 ׀неравенство Бернулли׀
׀неравенство Бернулли׀ 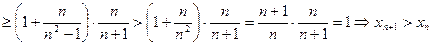
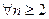 ,а это и означает, что последовательность
,а это и означает, что последовательность  убывает.
убывает.
Ограниченность снизу следует из неравенства 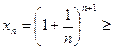 ׀неравенство Бернулли׀
׀неравенство Бернулли׀ 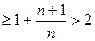 для всех натуральных значений n.
для всех натуральных значений n.
По теореме 1 существует 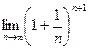 , который обозначают буквой е. Поэтому
, который обозначают буквой е. Поэтому 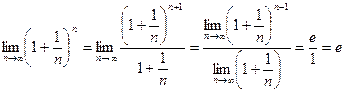 .
.
Число е иррационально и трансцендентно, е = 2,718281828… . Оно является, как известно, основанием натуральных логарифмов.
Замечания. 1) Неравенство Бернулли можно использовать для доказательства того, что 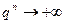 при
при 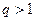 . Действительно, если
. Действительно, если 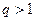 , то
, то 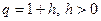 . Тогда, по неравенству Бернулли,
. Тогда, по неравенству Бернулли, 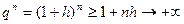 при
при 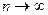 . Отсюда при
. Отсюда при 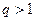 имеем
имеем 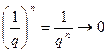 , то есть
, то есть 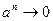 при
при 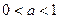 .
.
2) В рассмотренном выше примере основание степени 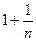 стремится к 1, а показатель степени n – к
стремится к 1, а показатель степени n – к 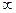 , то есть имеет место неопределенность вида
, то есть имеет место неопределенность вида 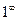 . Неопределенность такого вида, как мы показали, раскрывается с помощью замечательного предела
. Неопределенность такого вида, как мы показали, раскрывается с помощью замечательного предела 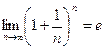 .
.
2) 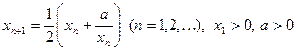 (*)
(*)
Докажем, что эта последовательность сходится. Для этого покажем, что она ограничена снизу и не возрастает. При этом воспользуемся неравенством 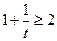 для всех
для всех 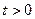 , которое является следствием неравенства
, которое является следствием неравенства 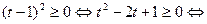
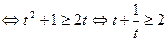 .
.
Имеем 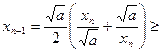 |см. неравенство выше|
|см. неравенство выше| 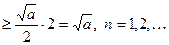 , т.е. последовательность ограничена снизу числом
, т.е. последовательность ограничена снизу числом 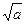 .
.
Далее, 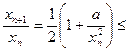 |так как
|так как 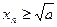 |
| 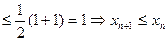 , т.е. последовательность не возрастает.
, т.е. последовательность не возрастает.
По теореме 1 существует 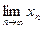 , который обозначим х. Переходя в равенстве (*) к пределу при
, который обозначим х. Переходя в равенстве (*) к пределу при 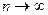 , получим
, получим
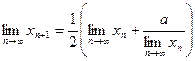 , т.е.
, т.е. 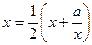 , откуда
, откуда 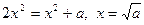 (берем знак «плюс», так как все члены последовательности положительны).
(берем знак «плюс», так как все члены последовательности положительны).
Последовательность (*) применяется при вычислении 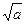 приближенно. За
приближенно. За 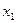 берут любое положительное число. Например, найдем
берут любое положительное число. Например, найдем 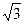 . Пусть
. Пусть 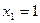 . Тогда
. Тогда 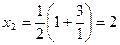 ,
, 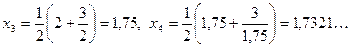 . Таким образом,
. Таким образом, 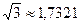 .
.
3) 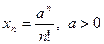 .
.
Имеем 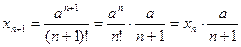 . Поскольку
. Поскольку 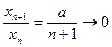 при
при 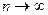 , существует номер N, такой, что для всех
, существует номер N, такой, что для всех 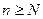 выполняется неравенство
выполняется неравенство 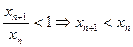 . Таким образом, последовательность
. Таким образом, последовательность  , начиная с некоторого номера N, убывает и ограничена снизу, так как
, начиная с некоторого номера N, убывает и ограничена снизу, так как 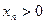 для всех значений n. Значит, по теореме 1 существует
для всех значений n. Значит, по теореме 1 существует 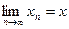 . Поскольку
. Поскольку 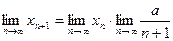 , имеем
, имеем 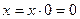 .
.
Итак, 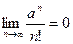 .
.
4) 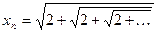 , справа – n корней.
, справа – n корней.
Методом математической индукции покажем, что 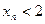 для всех значений n. Имеем
для всех значений n. Имеем 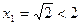 . Пусть
. Пусть 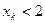 . Тогда
. Тогда 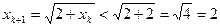 , отсюда получаем утверждение по принципу математической индукции. Используя этот факт, находим
, отсюда получаем утверждение по принципу математической индукции. Используя этот факт, находим 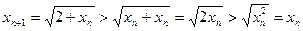 , т.е. последовательность
, т.е. последовательность  возрастает и ограничена сверху. Поэтому существует
возрастает и ограничена сверху. Поэтому существует 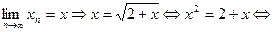
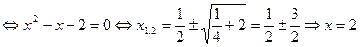 , так как
, так как 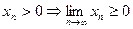 .
.
Таким образом, 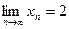 .
.
Дата добавления: 2016-06-09; просмотров: 24830;











