Числовые множества, их границы

Действительные числа изображаются, как известно, точками числовой прямой, причем каждому действительному числу соответствует одна точка числовой прямой и обратно, каждой точке числовой прямой соответствует только одно действительное число. Как говорят, установлено взаимно-однозначное соответствие между множеством точек числовой прямой и множеством действительных чисел. Поэтому, говоря о числовых множествах, мы будем иметь в виду как подмножества множества R действительных чисел, так и подмножества точек числовой прямой.

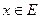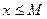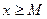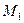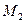Определение 1. Множество Е действительных чисел называется ограниченным сверху (соответственно, ограниченным снизу), если существует число М, такое, что для любого имеет место неравенство (соответственно, ). Число М называется верхней (соответственно, нижней) границей (или гранью) множества Е. Множество Е называется ограниченным, если существуют такие числа и , что для любого числа 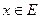имеет место двойное неравенство .

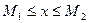Например, множество правильных дробей ограничено сверху числом 1, множество N натуральных чисел ограничено снизу числом 1, множество 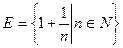ограничено, так как .

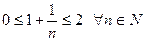Заметим, что если М – верхняя граница непустого ограниченного сверху числового множества Е, то любое число, большее М, также будет его верхней границей, то есть у Е есть бесконечное множество верхних границ. Из всех верхних границ множества Е наибольший интерес представляет его наименьшая верхняя граница.

Определение 2. Наименьшая из верхних границ множества Е называется его точной верхней границей (или точной верхней гранью) и обозначается sup E (от латинского слова supremum – наивысшее).

Аналогично вводится понятие точной нижней границы множества Е, ограниченного снизу.

Определение 3. Наибольшая из нижних границ множества Е называется его точной нижней границей (или точной нижней гранью) и обозначается inf E (от латинского слова infimum – наинизшее).

Имеет место

Теорема 1. Всякое непустое и ограниченное сверху (соответственно, снизу) числовое множество Е имеет точную верхнюю (соответственно, нижнюю) границу.

Доказательство. Проведем его для случая верхней границы. Рассмотрим два случая.

1) Предположим сначала, что среди чисел х множества Е найдется наибольшее 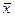. Тогда все числа множества будут удовлетворять неравенству 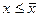, т.е. 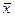– верхняя граница множества Е. С другой стороны, поскольку , то для любой верхней границы М выполняется неравенство 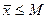. Отсюда следует, что 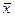– точная верхняя граница множества Е.

2) Пусть теперь среди чисел х множества Е нет наибольшего. Произведем сечение множества R действительных чисел следующим образом. К верхнему классу 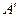отнесем все верхние границы 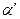множества Е, а к нижнему классу А все остальные действительные числа 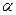. При этом все числа 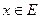попадут в класс А, так как среди них нет наибольшего. По теореме Дедекинда существует действительное число 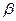, производящее данной сечение. Все числа 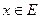, как принадлежащие классу А, не превосходят этого пограничного числа 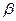, т.е. 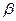– верхняя граница множества Е, т.е. 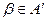и является в 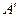наименьшим числом по теореме Дедекинда. Поэтому .

Аналогично доказывается вторая часть теоремы о существовании точной нижней границы (это могут сделать студенты дома самостоятельно). Теорема доказана.

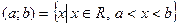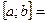
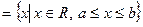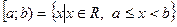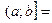
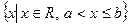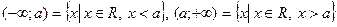Из школьного курса математики известны некоторые специальные числовые множества: – интервал (открытый промежуток), – отрезок (замкнутый промежуток), , – полуинтервалы (открытый справа и слева соответственно), – вся числовая прямая, – лучи. Отрезки, интервалы и полуинтервалы называются промежутками.

Определение 4. Если а – некоторое действительное число, 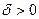– любое положительное действительное число, то интервал 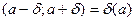называется 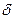- окрестностью точки а. Точка а называется центром окрестности, а число 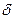- радиусом окрестности. Множество 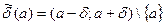называется проколотой 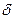- окрестностью точки а.