Графический способ.
Определение 9. Графиком функции 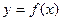 , заданной на множестве Х, называется множество всех точек плоскости
, заданной на множестве Х, называется множество всех точек плоскости 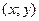 , координаты которых х и у связаны соотношением
, координаты которых х и у связаны соотношением 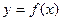 . Равенство
. Равенство  называется уравнением этого графика.
называется уравнением этого графика.
Функция считается заданной графически, если начерчен ее график. Например, для измерения давления атмосферы на различных высотах используется специальный самопишущий аппарат – барограф, который на движущейся ленте записывает в виде кривой изменение давления в зависимости от высоты.
Не всякая кривая может служить графиком некоторой функции. Необходимо, чтобы не содержалось на ней никаких двух точек с одинаковыми абсциссами.
|
|
|


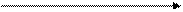
|
|
|


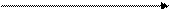
Кривая определяет Кривая не определяет
функцию никакой функции
Преимущество графического способа задания функции перед другими – в наглядности, недостаток в том, что значения функции можно найти лишь приближенно. Не для всякой функции можно построить график. Например, нельзя изобразить графически функцию Дирихле (Петер Густав Лежен-Дирихле (1805-1859) – немецкий математик)
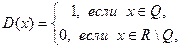
так как между любыми двумя значениями х имеется бесконечно много как рациональных, так и иррациональных точек.
Словесный способ.Функция задается словами. Например, целая часть числа х – это наибольшее целое число, не превосходящее х.
Определение 10. Функции 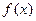 и
и 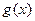 , заданные на некотором промежутке Х, называются тождественно равными на этом промежутке:
, заданные на некотором промежутке Х, называются тождественно равными на этом промежутке: 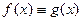 , если их значения в каждой точке
, если их значения в каждой точке 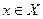 совпадают.
совпадают.
Пример. Тождественны ли функции:
1) 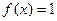 и
и 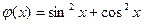 ;
;
2) 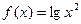 и
и 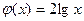 для
для 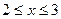 ;
;
3) 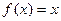 и
и 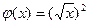 ?
?
Решение. 1) 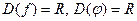 , т.е.
, т.е. 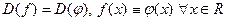 , т.е. функции тождественно равны.
, т.е. функции тождественно равны.
2) 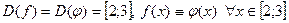 по свойству
по свойству 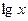 .
.
3) 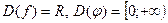 , т.е.
, т.е. 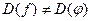 , функции не являются тождественно равными.
, функции не являются тождественно равными.
Дата добавления: 2016-06-09; просмотров: 3200;











