Композиция отображений. Понятие действительной функции

Понятие отображения множеств играет важную роль во всех областях математики.

Определение 1. Пусть Х и Y – некоторые множества и 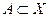. Если каждому элементу 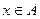поставлен в соответствие один и только один элемент 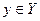, то говорят, что задано отображение из Х в Y с областью задания А.

Отображения обычно обозначают малыми латинскими буквами .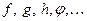

Пример 1. Пусть Х – множество натуральных чисел, 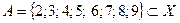. Каждому числу 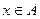поставим в соответствие остаток от его деления на 2: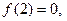 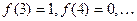. Получим отображение из Х в множество действительных чисел R, при котором каждому 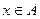соответствует либо 0, либо 1.

Множество Х называют также множеством отправления, а множество Y – множеством прибытия.

Определение 2. Элемент 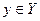, соответствующий элементу 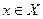в отображении f, называется образомэлемента х и обозначается 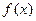. При этом сам элемент х называется прообразом элемента у. Если А – область задания при отображении f, то множество 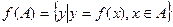называют образом множества А при отображении f или областью значений отображения f.

Определение 3. Если область задания совпадает с областью отправления, т.е 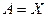, то f называют отображением Х в Y обозначают 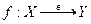. Если 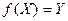, то f называют отображением Х на Y.

Определение 4. Отображение 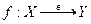называется обратимым, если разным элементам 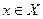соответствуют различные элементы 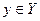, т.е. для любых 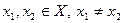имеем .

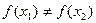Например, отображение 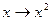с областью задания R не является обратимым, так как 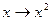и 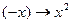, т.е. 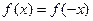, хотя .

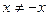Определение 5. Обратимое отображение Х на Y называется взаимно однозначным отображением.

Введенные понятия проиллюстрируем рисунками.

f не является отображением д)

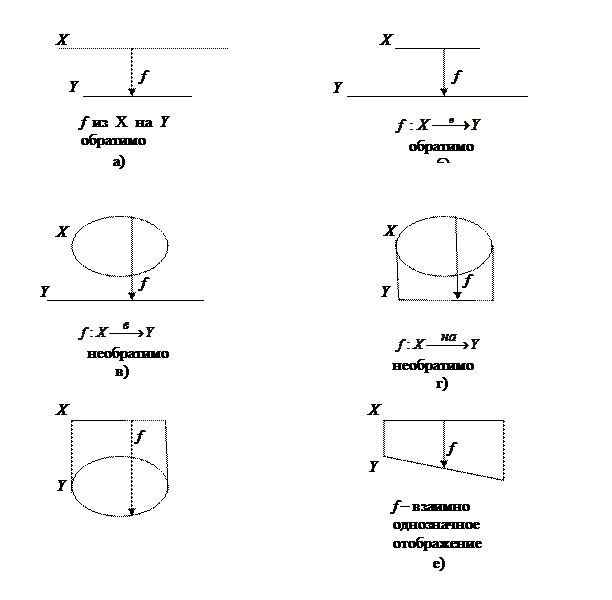
Пусть f – обратимое отображение из Х в Y с областью задания А. Тогда каждому элементу 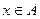соответствует один и только один элемент 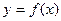, причем разным элементам 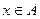соответствуют различные элементы у. Поэтому определено отображение 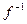множества 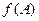в Х (на А). Определено так, что .

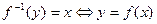Определение 6. Если отображение f из Х в Y обратимо, то отображение 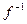из Y в Х, определяемое соотношением 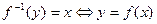, называется обратным к f .

Пусть теперь f – отображение Х в Y, а g – отображение Y в Z. Определим отображение Х в Z следующим образом: 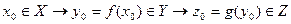. Таким образом, 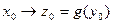, то есть 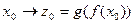. Такое отображение называется композицией отображений f и g и обозначается 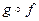. Итак, для всех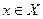

.

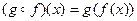Операция композиции отображений обладает следующими свойствами.

1) Ассоциативность:

.

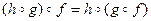Действительно, если 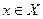, то

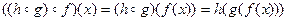и .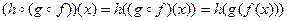

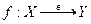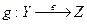2) Если отображения и обратимы, то и их композиции обратима, причем

.

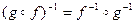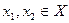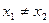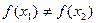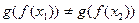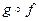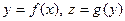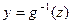Действительно, пусть и . В силу обратимости f . В силу обратимости g и, значит, отображение обратимо. Если , то , а 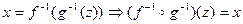, то есть 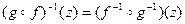, что и требовалось доказать.

Действительная функция есть частный случай отображения, когда множества X и Y являются числовыми множествами.

Определение 7. Пусть X – числовое множество. Отображение 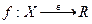, сопоставляющее каждому числу 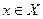число 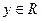, называется действительной функцией, заданной на множестве Х. При этом х называется аргументом функции f, Х – областью ее определения, 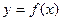– значением функции. Множество 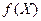называется множеством значений функции.

Определение 8. Если функция f ставит в соответствие каждому числу 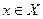одно и то же значение а, то функцию f называют постоянной.

Из определения действительной функции следует, что для задания функции f надо задать ее область определения – множество Х и закон, по которому каждому числу 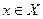ставится в соответствие число .

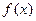В зависимости от того, каким образом задается закон функциональной зависимости, различают несколько способов задания функции.

Аналитический способ.Закон функциональной зависимости задается с помощью формулы, указывающей, какие действия нужно произвести над аргументом х, чтобы получить значение функции.

Примеры: 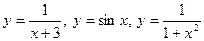и т.д.

В случае аналитического способа задания функции множество Х часто не указывают. Областью определения функции в этом случае считают естественную область определения функции – множество значений аргумента, для которых имеет смысл данное аналитической выражение.

Например, для функции 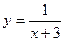область определения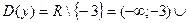 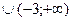, для функции .

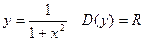Если функция отражает зависимость между конкретными величинами (физическими, геометрическими и другими), то область ее определения может не совпадать с той областью, где формула имеет смысл. Например, функция 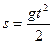, рассматриваемая абстрактно, определена на R, если же она выражает закон свободного падения тела, то .

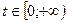Заметим, что функция может быть задана не одной, а несколькими формулами.

Например, 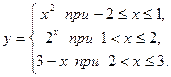Для этой функции .

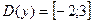Табличный способ.При этом способе задания закон функциональной зависимости устанавливается таблицей, в которой различным значениям аргумента сопоставлены соответствующие значения функции.

Табличный способ используется в экспериментальных исследованиях, когда, например, снимаются показания приборов через определенные промежутки времени.

Составлены таблицы значений многих функций, часто применяемых при технических расчетах, которые позволяют находить значения функций без вычислений.

Недостаток табличного способа состоит в том, что по таблице можно найти значения функции только для тех значений аргумента, которые в ней есть. Другие значения можно находить с помощью интерполирования приближенно.