Теорема Больцано-Вейерштрасса. Принцип сходимости

Определение 1. Пусть дана некоторая числовая последовательность

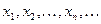. (7.1)

Если из этой последовательности выписывать не все члены подряд, а с пропуском, то получим новую последовательность

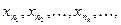(7.2)

которая называется частичной последовательностью или подпоследовательностью по отношению к последовательности (7.1).

Порядковый номер члена 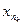в (7.2) определяется уже не числом n, а числом k и 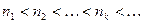. Очевидно, что 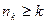, причем 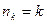тогда и только тогда, когда в (7.2) включены все первые k членов последовательности (7.1) без пропусков.

Теорема 1. Если последовательность (7.1) имеет своим пределом число а, то любая ее подпоследовательность (7.2) тоже имеет предел, равный а.

Доказательство. Пусть последовательность (7.1) сходится к числу а. Это значит, что для любого 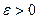найдется номер N, такой, что для всех значений 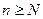выполняется неравенство 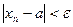. Поскольку 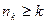, то для всех 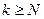будет 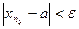, т.е. 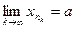. Теорема доказана.

Замечание. Доказанную теорему удобно применять при доказательстве того, что последовательность 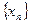не имеет предела. Для этого достаточно найти две ее подпоследовательности, имеющие разные пределы. Например, для последовательности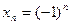 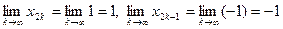, поэтому данная последовательность предела не имеет.

В приведенном примере сама последовательность предела не имеет, однако существуют подпоследовательности, имеющие конечный предел. Будет ли так для любой последовательности? Для неограниченной последовательности нет, например, из последовательности 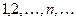нельзя извлечь сходящуюся подпоследовательность. Для ограниченных же последовательностей справедлива

Теорема 2 (Больцано (1781-1848)-Вейерштрасса (1815-1897)). Из любой ограниченной последовательности всегда можно извлечь сходящуюся подпоследовательность.

Доказательство. Пусть последовательность 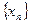ограничена. Тогда найдется отрезок 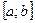, такой, что 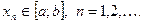Разделим 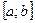пополам точкой 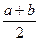и выберем тот из частичных отрезков, который содержит бесконечно много членов последовательности. Если такими являются оба отрезка, то возьмем любой из них. Обозначим его 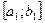. Разделим 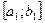пополам точкой 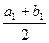и через 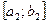обозначим ту из его половин, которая содержит бесконечно много членов последовательности. Продолжая этот процесс, получим стягивающуюся систему вложенных отрезков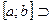 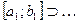, так как 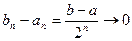при 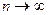. По принципу вложенных отрезков существует точка с, принадлежащая всем этим отрезкам. Пусть 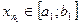– любой член последовательности 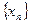, 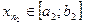– любой член последовательности 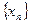, 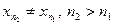и т.д. Так мы построим подпоследовательность 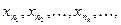причем 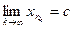, так как 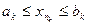, а . 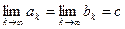Теорема доказана.

При определении сходящееся последовательности мы использовали число а (предел последовательности). Нельзя ли определить, сходится последовательность или нет, по виду ее членов, не используя никаких других чисел? Оказывается можно. Справедлива

Теорема 3 (критерий Коши или принцип сходимости). Для того чтобы последовательность 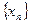была сходящейся, необходимо и достаточно, чтобы для любого 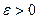существовал такой номер N, что 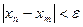для всех .

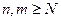Без доказательства.

Определение 2. Последовательность 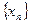, удовлетворяющая условию теоремы Коши, т.е. последовательность такая, что для любого 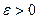существует такой номер N, что 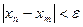для всех 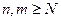, называется фундаментальной.

Поэтому теорему 3 можно сформулировать так:

Теорема 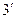. Для того чтобы последовательность 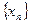была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.

Рассмотрим пример применения теоремы Коши.

Пусть 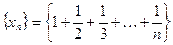. Покажем, что эта последовательность не является фундаментальной и, следовательно, расходится в силу теоремы Коши.

Рассмотрим 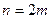. Тогда

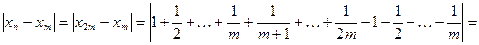
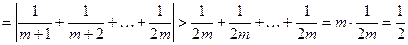
для всех 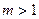. Это означает, что для 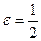, какой бы номер N мы ни брали, неравенство 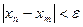для всех 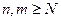не выполняется, т.е. последовательность 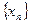не является фундаментальной и, значит, расходится.