Абсолютная устойчивость
Рассмотрим понятие абсолютной устойчивости применительно к структуре нелинейной системы рис. 2.2.
Уравнения, описывающие поведение системы при 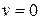 имеют в соответствии с [8] вид
имеют в соответствии с [8] вид
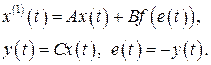 (2.72)
(2.72)
Будем полагать, что 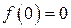 , тогда уравнения имеют тривиальное решение
, тогда уравнения имеют тривиальное решение 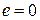 ,
, 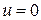 ,
, 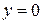 , т.е. в системе существует положение равновесия, устойчивость которого будем исследовать.
, т.е. в системе существует положение равновесия, устойчивость которого будем исследовать.
Если положение равновесия системы (2.72) асимптотически устойчиво в целом при любом виде функции 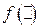 из заданного класса, то САУ называется абсолютно устойчивой в этом классе.
из заданного класса, то САУ называется абсолютно устойчивой в этом классе.
Будем рассматривать класс функций 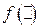 , удовлетворяющих секторным ограничениям, т.е. с характеристикой
, удовлетворяющих секторным ограничениям, т.е. с характеристикой 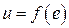 , построенной на плоскости
, построенной на плоскости 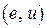 , которая полностью укладывается в угловом секторе, образованном двумя прямыми
, которая полностью укладывается в угловом секторе, образованном двумя прямыми 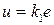 и
и 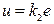 ,
, 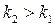 .
.
Итак, рассматривается класс нелинейных функций, удовлетворяющих условиям
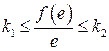 для
для 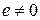 ,
, 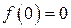 . (2.73)
. (2.73)
При этом вид функции 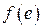 неизвестен, а нелинейность будет относиться к классу
неизвестен, а нелинейность будет относиться к классу 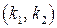 . Возможны также дополнительные ограничения, например, функция
. Возможны также дополнительные ограничения, например, функция 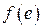 должна быть непрерывной или другие.
должна быть непрерывной или другие.
Из класса (2.73) выделяют два подкласса: 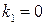 и
и 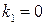 ,
, 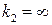 .
.
Анализ абсолютной устойчивости возможен с помощью функций Ляпунова, а также частотных критериев абсолютной устойчивости. Рассмотрим последние как наиболее практичные.
Круговой критерий устойчивости.
Для нелинейностей из класса 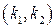 достаточным условием абсолютной устойчивости является выполнение неравенства
достаточным условием абсолютной устойчивости является выполнение неравенства
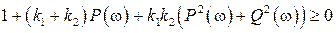 , (2.74)
, (2.74)
где 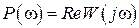 ,
, 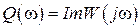 ,
, 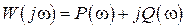 − АФЧХ линейной части системы (рис. 2.2).
− АФЧХ линейной части системы (рис. 2.2).
Неравенство (2.74) определяет область на комплексной плоскости, в которой должна лежать АФЧХ линейной части системы, чтобы нелинейная система была абсолютно устойчива.
Заменяя в (2.74) знак неравенства на знак равенства, получим границу этой области. Это будет уравнение окружности с центром на вещественной оси в точке 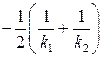 и проходящей через точки
и проходящей через точки 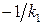 и
и 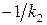 на оси
на оси 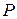 . Неравенство (2.74) требует, чтобы АФЧХ при всех
. Неравенство (2.74) требует, чтобы АФЧХ при всех 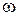 располагалась вне круга, ограниченного этой окружностью. На рис. 2.20 приведены запретные области (заштрихованные) для характеристики
располагалась вне круга, ограниченного этой окружностью. На рис. 2.20 приведены запретные области (заштрихованные) для характеристики 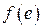 и характеристики
и характеристики 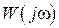 .
.

Рис. 2.20
В [4] даются более подробные случаи для разных классов 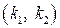 .
.
Вторым распространенным частотным критерием является критерий В.М. Попова. Рассмотрим его формулировку для класса нелинейных характеристик 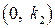 : система будет абсолютно устойчивой для нелинейностей из класса
: система будет абсолютно устойчивой для нелинейностей из класса 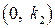 , если через точку
, если через точку 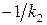 можно провести прямую так, что она не пересечет модифицированную частотную характеристику (последняя лежит справа от прямой).
можно провести прямую так, что она не пересечет модифицированную частотную характеристику (последняя лежит справа от прямой).
В этом критерии под модифицированной частотной характеристикой понимается характеристика 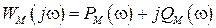 , где
, где 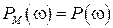 ,
, 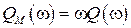 .
.
Рис. 2.21, а удовлетворяет критерию абсолютно устойчивой системы, а рис. 2.21, б при заданном 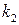 не удовлетворяет этому критерию.
не удовлетворяет этому критерию.
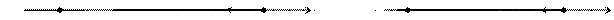
Рис. 2.21
В заключение отметим, что все критерии абсолютной устойчивости, в том числе частотные, дают только лишь достаточные условия абсолютной устойчивости.
Дата добавления: 2022-02-05; просмотров: 860;











