Вынужденные колебания в нелинейных системах

Рассмотрим НСАУ, структурная схема которой приведена на рис. 2.2, в режиме вынужденных движений, когда на вход системы подается сигнал 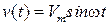. Будем искать решение в виде .

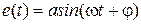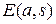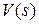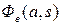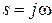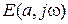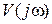Для гармонически линеаризованной системы используем связь изображения ошибки и входного воздействия через передаточную функцию замкнутой системы по ошибке . Сделав замену и подставив значения и в показательной форме, получим

.

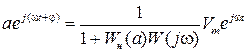После очевидных преобразований имеем

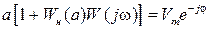. (2.67)

Здесь 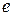– основание натурального логарифма.

Для определения решений (2.67) строится в системе координат линейной части системы зависимость, соответствующая левой части (2.67) (обозначим ее А)и окружность радиуса 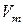с центром в начале координат (рис. 2.19, а). Точка пересечения 1 дает искомые значения 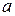и 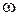. Колебания будут устойчивы (т.е. в НСАУ возникнут автоколебания), если при росте 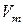возрастает значение .

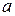В нелинейных системах наличие автоколебаний зависит от величины внешнего воздействия. Если кривая А начинается не в начале координат, то режим в НСАУ зависит от пороговой величины внешнего воздействия 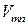(рис. 2.19, б).

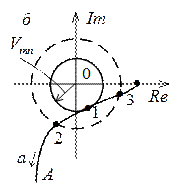
Рис. 2.19

Значение 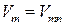соответствует точке 1 касания окружности линии А. Эта граница раздела движений на колебания (автоколебания), когда 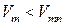и вынужденные колебания, когда 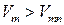. Они могут быть устойчивыми (точка 2) и неустойчивыми (точка 3).