Абсолютная и относительная погрешности

Пример 1.1.

Если x = 0,00006, а 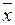= 0,00005, то e_x = 0,00001, а δ_х = 0,2 или 20%

Пример 1.2.

Если x = 100500, а 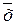= 100000, то e_х = 500, а δ_х = 0,005 или 0,5%

Пример 1.3.

Используя Mathcad, найти предельные абсолютные и относительные погрешности чисел x = 984,6 и x = 2,364, если они имеют только верные цифры: а) в строгом смысле, б) в широком смысле

Решение примера 1.3 приведено на рис.1.1

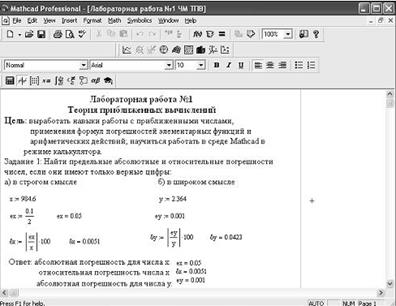
Рис. 1.1. Фрагмент рабочего документа Mathcad для выполнения примера 1.3

Пример 1.4.

Задано число x = 2,3644 и относительная погрешность δ_х = 0,07%. Определить количество верных цифр числа по относительной погрешности.

Решение.

δ_х = 0,0007 < 10^-3, значит, число х имеет, по крайней мере, две цифры, верных в строгом смысле. Вычислим

Δх = 24,307 ∙ 0,0007 = 0,0170149 < 0,05.

То есть, в строгом смысле действительно верны цифры 2 и 3.

Пример 1.5.

Пусть х = 984,6, δ_х = 0,008. Определить количество верных цифр в числе х.

Решение.

Очевидно, что 0,008 < 0,01 = 10^-2. Это означает, что число х имеет, по крайней мере, одну верную в строгом смысле цифру (цифра 9). Полученный результат легко подтвердить, используя определение цифры, верной в строгом смысле.

Вычислим е_х = 984,6 ∙ 0,008 = 7,8768. Полученная абсолютная погрешность не превышает половину единицы разряда сотен. Откуда следует, что цифра 9 действительно верна в строгом смысле, как по относительной погрешности, так и по абсолютной.

Пример 1.6.

Пусть х = 24,307, δ_х = 0,005 %. Определить все верные цифры числа.

Решение.

δ_х = 0,00005 = 0,5 ∙ 10^-4, значит, в х, по крайней мере, четыре цифры верны в строгом смысле. Вычислим Δх = 24,307 ∙ 0,00005 = 0,00121535 < 0,005.

То есть верными цифрами будут являться цифры 2, 4, 3, 0.

Пример 1.7.

Дано число х = 24,010. Цифры верны в строгом смысле. Указать границы его абсолютной и относительной погрешности.

Решение.

Из определения цифры, верной в строгом смысле, можно заключить, что абсолютная погрешность числа х не превосходит половины единицы разряда тысячных. Значит, е_х = 0,0005.

Относительную погрешность найдем по формуле:

δ_х = 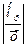= = 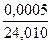0,2 ∙ 10^-4 = 0,2 ∙ 10^-2 %.

Пример 1.8.

При взвешивании двух грузов получили следующие значения их масс

х = 0,5 кг, y = 50 кг. Считая абсолютную погрешность взвешивания равной 1 г, определить относительную погрешность измерения масс тел х, у. Какое из тел взвешено более точно?

Решение.

Относительную погрешность найдем по формулам:

δ_х = 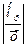= = 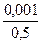2 ∙ 10^-3 = 0,2%.

δ_y = 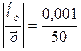= 2 ∙ 10^-5 = 0,002%.

Более точно измерен груз весом 50 кг.