Абсолютная и относительная погрешность
Учет погрешностей является важным аспектом применения численных методов, поскольку погрешность конечного результата решения всей задачи является продуктом взаимодействия всех видов погрешностей. Поэтому одной из основных задач теории погрешностей является оценка точности результата на основании точности исходных данных.
Если 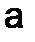 – точное число и
– точное число и 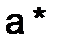 – его приближенное значение, то погрешностью (ошибкой) приближенного значения
– его приближенное значение, то погрешностью (ошибкой) приближенного значения 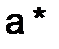 является степень близости его значения к его точному значению
является степень близости его значения к его точному значению 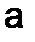 .
.
Простейшей количественной мерой погрешности 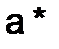 является абсолютная погрешность, которая определяется как
является абсолютная погрешность, которая определяется как
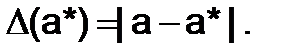 (6.1.2-1)
(6.1.2-1)
Как видно из формулы 6.1.2-1, абсолютная погрешность имеет те же единицы измерения, что и величина 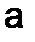 . Поэтому по величине абсолютной погрешности далеко не всегда можно сделать правильное заключение о качестве приближения. Например, если
. Поэтому по величине абсолютной погрешности далеко не всегда можно сделать правильное заключение о качестве приближения. Например, если 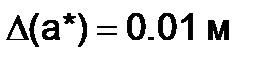 , а речь идет о детали станка, то измерения являются очень грубыми, а если о размере судна, то – очень точными. В связи с этим введено понятие относительной погрешности, в котором значение абсолютной погрешности отнесено к модулю приближенного значения (
, а речь идет о детали станка, то измерения являются очень грубыми, а если о размере судна, то – очень точными. В связи с этим введено понятие относительной погрешности, в котором значение абсолютной погрешности отнесено к модулю приближенного значения (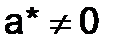 ).
).
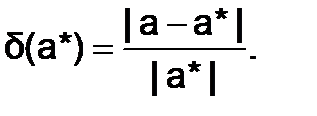 (6.1.2-2) Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерений данных. Относительная погрешность измеряется в долях или процентах. Так, например, если
(6.1.2-2) Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерений данных. Относительная погрешность измеряется в долях или процентах. Так, например, если
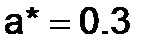 , а
, а 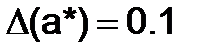 , то
, то 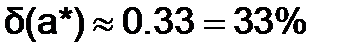 , а если
, а если 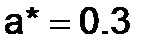 и
и 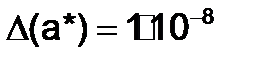 ,
,
то тогда 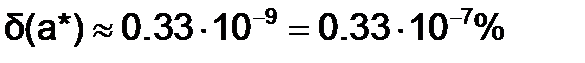 .
.
Чтобы численно оценить погрешность функции, требуется знать основные правила подсчета погрешности действий:
· при сложении и вычитании чисел абсолютные погрешности чисел складываются
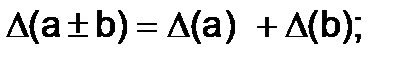
· при умножении и делении чисел друг на друга складываются их относительные погрешности
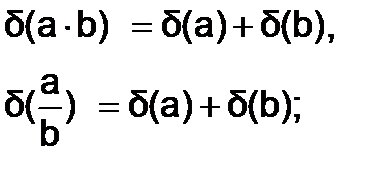
· при возведении в степень приближенного числа его относительная погрешность умножается на показатель степени
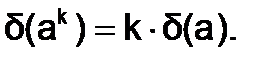
Пример 6.1.2-1. Дана функция: 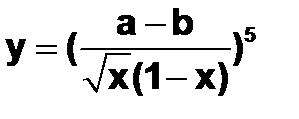 . Найти абсолютную и относительную погрешности величины
. Найти абсолютную и относительную погрешности величины  (погрешность результата выполнения арифметических операций), если значения
(погрешность результата выполнения арифметических операций), если значения 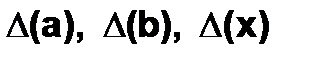 известны, а 1 – точное число и его погрешность равна нулю.
известны, а 1 – точное число и его погрешность равна нулю.

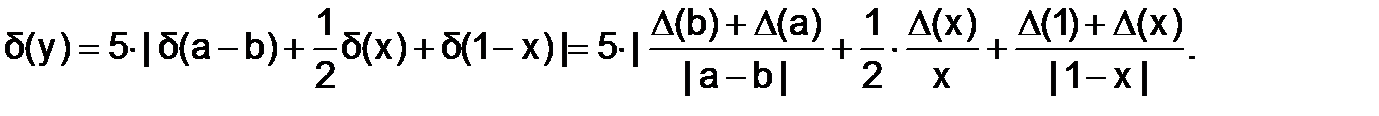
Определив, таким образом, значение относительной погрешности, можно найти значение абсолютной погрешности, как 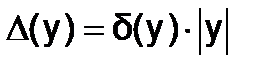 , где величина
, где величина 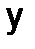 вычисляется по формуле при приближенных значениях
вычисляется по формуле при приближенных значениях 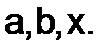
Поскольку точное значение величины 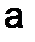 обычно неизвестно, то вычисление
обычно неизвестно, то вычисление 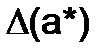 и
и 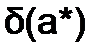 по приведенным выше формулам невозможно. Поэтому на практике проводят оценку предельных погрешностей вида:
по приведенным выше формулам невозможно. Поэтому на практике проводят оценку предельных погрешностей вида:
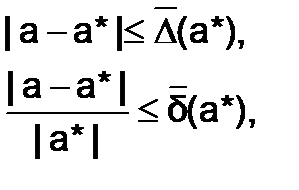 (6.1.2-3)
(6.1.2-3)
где 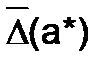 и
и 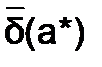 – известные величины, которые являются верхними границами абсолютной и относительной погрешностей, иначе их называют – предельная абсолютная и предельная относительная погрешности. Таким образом, точное значение
– известные величины, которые являются верхними границами абсолютной и относительной погрешностей, иначе их называют – предельная абсолютная и предельная относительная погрешности. Таким образом, точное значение 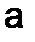 лежит в пределах:
лежит в пределах: 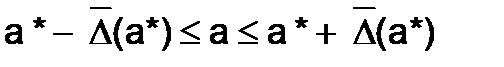 или
или 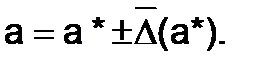

Если величина 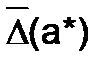 известна, то
известна, то 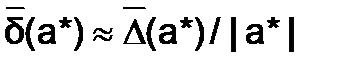 , а если известна величина
, а если известна величина 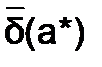 , то
, то 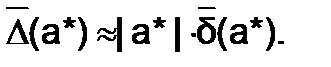
Предельная абсолютная погрешность функции вида 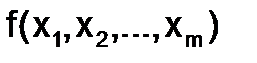 , дифференцируемой в заданной области, при известных значениях аргументов
, дифференцируемой в заданной области, при известных значениях аргументов 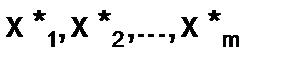 , а также при известных предельных абсолютных погрешностях аргументов
, а также при известных предельных абсолютных погрешностях аргументов 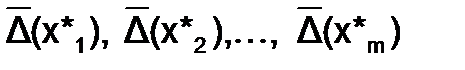 , вычисляется по формуле:
, вычисляется по формуле:
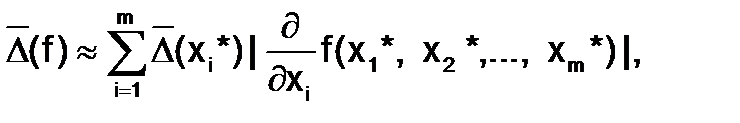 (6.1.2-4)
(6.1.2-4)
а, соответственно, предельная относительная погрешность функции
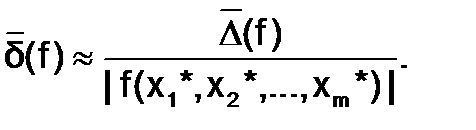 (6.1.2-5)
(6.1.2-5)
В частном случае для функции от одной переменной (при m=1):
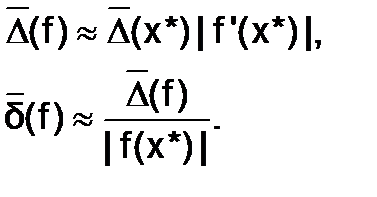
Пример 6.1.2-2. Оценить абсолютную и относительную погрешности приближенного числа 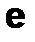 .
.
Число 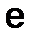 – трансцендентное число, представляется бесконечной непериодической дробью
– трансцендентное число, представляется бесконечной непериодической дробью  .
.
Приближенное значение числа 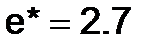 .
.
Граница абсолютной погрешности 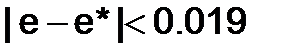 , относительная погрешность числа
, относительная погрешность числа 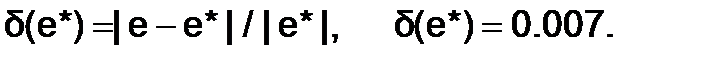
Дата добавления: 2021-05-28; просмотров: 855;











