Гомологии на расширенной плоскости

Рассмотрим случаи гомологии с несобственными элементами на расширенной евклидовой плоскости.

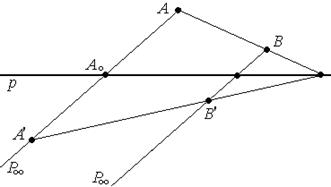
1. Р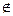_∞ р .

А, А′ коллинеарны с Р_∞ , В и В′ также коллинеарны с Р_∞ (АА′)||(ВВ′).

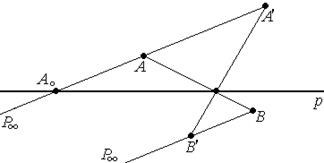
h = (Р_∞А₀ , АА′)=( АА′, Р_∞А₀)=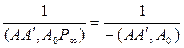

Т.е. (АА′, А₀)= - 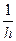- константа, а значит сохраняется простое отношение трех точек, т.е. гомология является родством.

Если кроме того гомология инволюционна, тогда (АА′, А₀)= 1

А₀ - середина отрезка АА′. Тогда это косая симметрия.

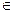2. Р_∞ р .

А, А′ коллинеарны с Р_∞ , В и В′ также коллинеарны с Р_∞ (АА′)||(ВВ′)|| р.

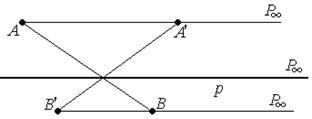
3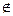. Р р_∞ .

(АА′)∩р_∞=А_0∞ , кроме того (АВ)∩(А′В′)=Х 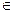р_∞ гомология является гомотетией с центром Р. Так как гомология гиперболическая, то h=(РА_0∞ , АА′)=(АА′, РА_0∞)= - (АА′, Р) (АА′,А₀)= - h = k - коэффициент гомотетии.

при h = -1 (АА′,А₀)= 1

Р - середина отрезка АА′ , а это центральная симметрия.

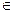4. Р р_∞ .

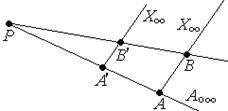
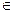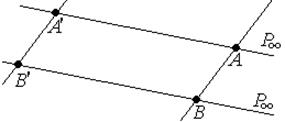
Так как Р р_∞ Р_∞ , но при Р_∞ → (АА′)||(ВВ′), а при р_∞ → (АВ)||(А′В′) гомология является параллельным переносом на вектор .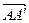

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

В дополнение к данному конспекту лекций можно порекомендовать следующую литературу:

1. Атанасян Л.С., Базылев В.Т. Геометрия. Ч.2. - М.: Просвещение, 1987. - 351 с.

2. Вернер А.Л., Кантор Б.Е., Франгулов С.А. Геометрия. Ч. 2. - СПб.: Специальная литература, 1997. - 320 с.

3. Жафяров А.Ж. Геометрия. Ч.2. - Новосибирск: Сибирское университетское изд-во, 2003. - 266 с.

4. Жафяров А.Ж., Абрамов А.В., Дмитриева А.В., Шрайнер Е.Г. Проективная геометрия. - Новосибирск: Изд-во НГПУ, 1995. - 132 с.

5. Певзнер С.Л. Проективная геометрия. - М.: Просвещение, 1980. – 128 с.