Построение образов и прообразов точек при инволюции прямой.
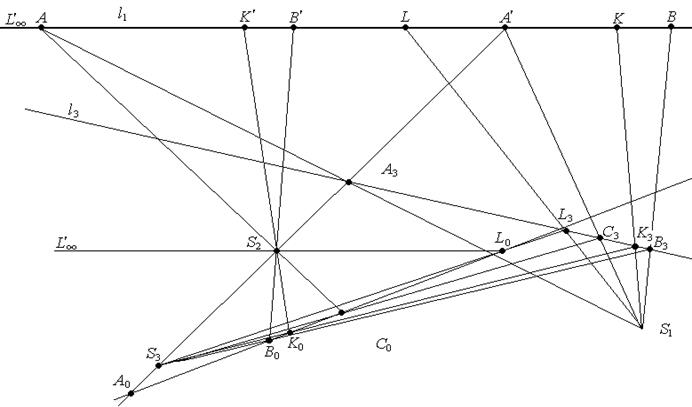
Задача. Инволюция задана точками А ↔ А′ и В ↔ В′. Построить образ и прообраз произвольных точек.
Решение. Решение соответствует второму случаю (ℓ1 = ℓ2) отображения φ: А → А′,В → В′, А′ → А.
Построение:
1. 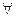 S1
S1 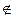 ℓ1 ,
ℓ1 ,
2. 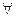 ℓ3 , такую, что S1
ℓ3 , такую, что S1 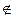 ℓ3 и ℓ1 ≠ ℓ3 ,
ℓ3 и ℓ1 ≠ ℓ3 ,
3. А3 = ℓ3 ∩ (S1 А), В3 = ℓ3 ∩ (S1В), С3 = ℓ3 ∩ (S1 А′),
4. 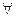 S2 ≠ S3
S2 ≠ S3 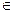 (А′А3),
(А′А3),
5. С0 =(S3С3)∩(S2А), В0 =(S3В3)∩(S2В′), А0 =(В0С0)∩(А′А3).
6. 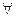 К К3 =ℓ3∩(S3 К), К0=(S3К3)∩(В0С0), К′=(S2К0)∩ℓ1 .
К К3 =ℓ3∩(S3 К), К0=(S3К3)∩(В0С0), К′=(S2К0)∩ℓ1 .
7. L∞ 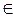 ℓ1, L0=(S2L3)∩(В0С0), L3=(S3L0)∩ℓ3, L=(S1L3)∩ℓ1.
ℓ1, L0=(S2L3)∩(В0С0), L3=(S3L0)∩ℓ3, L=(S1L3)∩ℓ1.
8. Построение прообразов в обратном порядке (самостоятельно).
Задача. Дана гиперболическая инволюция и даны инвариантные точки М1 и М2 . Построить образ и прообраз произвольной точки А.
 Решение. По свойству (4) → (АА′, М1М2)= - 1. Т.о. задача сводится к построению четвертой гармонической точки. Аналогично строится прообраз точки.
Решение. По свойству (4) → (АА′, М1М2)= - 1. Т.о. задача сводится к построению четвертой гармонической точки. Аналогично строится прообраз точки.
Задача. Даны точки А 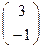 ↔ А′
↔ А′ 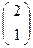 и В
и В 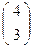 ↔ В′
↔ В′ 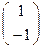 . Найти уравнение инволюции.
. Найти уравнение инволюции.
Решение. Пусть матрица инволюции М=  , тогда формулы λ∙Х ′ = М∙Х и λ∙Х = М∙Х ′.
, тогда формулы λ∙Х ′ = М∙Х и λ∙Х = М∙Х ′.
Подставим точки:
λ1∙А′=М∙А 
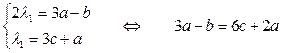 ,
,
λ2∙А=М∙А′ 
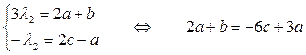 ,
,
λ3∙В′=М∙В 
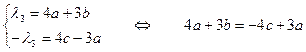 ,
,
λ4∙В=М∙В′ 
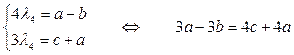 .
.
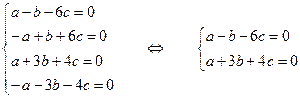 .
.
Одно из решений а = 7, b= - 5, с= 2,  М=
М= 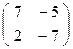 .
.
Уравнение инволюции: λ∙Х ′ = 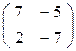 ∙Х.
∙Х.
Задача. Известны неподвижные точки инволюции - М1 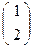 и М2
и М2 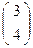 , найти её уравнение.
, найти её уравнение.
Решение. Пусть матрица инволюции М= 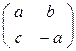 ,
,
тогда формулы преобразования λ∙Х′=М∙Х и λ∙Х=М∙Х′, для инвариантных точек λ∙Х=М∙Х .
Подставим наши точки: λ1∙М1=М∙М1, λ2∙М2=М∙М2 .
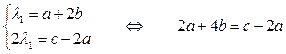
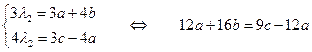
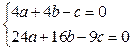 .
.
Одно из решений а = -5, b= 3, с= - 8,  М=
М= 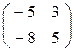 .
.
Уравнение инволюции: λ∙Х ′ = 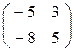 ∙Х .
∙Х .
Задача. Найти неподвижные точки инволюции 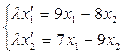 .
.
Решение. Матрица инволюции М= 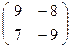 .
.
Тогда характеристическое уравнение λ 2 - 92–(-8)∙7 = 0  λ 2= 25
λ 2= 25  λ = ± 5.
λ = ± 5.
При λ1 = 5, 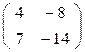 ∙
∙ 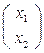 =
= 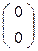

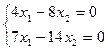
 х1 = 2∙х2 ,
х1 = 2∙х2 ,  М1 =
М1 = 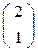 .
.
При λ 2 = -5 , 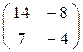 ∙
∙ 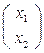 =
= 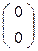

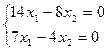
 7∙х1 = 4∙х2 ,
7∙х1 = 4∙х2 ,  М2 =
М2 = 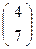 .
.
Коллинеация
Определение: Проективное преобразование плоскости называется коллинеацией, если образом точки будет точка, а образом прямой прямая.
Свойства:
1. Сохраняется инцидентность точек и прямых.
2. Сохраняется сложное отношение четырёх точек, лежащих на одной прямой и четырёх прямых пучка.
3. Композиция коллинеаций, есть коллинеация.
4. Множество коллинеаций образует подгруппу в группе проективных преобразований.
Доказательство. Самостоятельно.
Теорема 1. Пусть А1, В1, С1, D1 и А2, В2, С2, D2 - упорядоченные четверки точек, в каждой из которых никакие три не лежат на одной прямой. Тогда существует коллинеация φ на проективной плоскости такая, что: φ(А1) = А2, φ(В1) =В2, φ(С1) = С2, φ(D1) = D2.
Доказательство. По аналогии с проективным отображением прямой на прямую, преобразование плоскости можно разложить на композицию не более чем трёх перспектив. Доказательство осуществляется построением. □
Рассмотрим Р2 и два репера, тогда уравнение коллинеации, переводящее точки репера в точки репера единственное и задается формулами (**).
Пусть и ( и1 : и2 : и3 ) - прямая и∙Х = 0, её образ - f (и) = и ′ (и′1 : и′2 : и′3) → и′∙Х ′ = 0 .
и∙Х = и∙А-1 ∙f (Х) = и∙А-1 ∙Х ′ = 0 → и∙А-1 = λ∙и′  μ∙и = и′∙А.
μ∙и = и′∙А.
Вывод:Формулы коллинеации имеют вид:
Для точек: λ∙Х ′=А∙Х и μ∙Х = А-1∙Х ′.
Для прямых: и∙А-1 = λ∙и′ μ∙и = и′∙А.
Замечание: Формулы очень похожи на формулы преобразования координат при переходе к другому реперу. Но там координаты одной и той же точки в разных реперах, здесь координаты разных точек (образа и прообраза) в одном репере.
Инварианты коллинеации
Определение: Точка называется неподвижной (инвариантной) точкой проективного преобразования, если она переходит сама в себя.
Определение: Прямая называется неподвижной (инвариантной) прямой проективного преобразования, если она переходит
сама в себя.
Определение: Прямая называется точечно неподвижной (точечно инвариантной) прямой проективного преобразования, если каждая точка этой прямой инвариантна.
Нахождение инвариантов коллинеации.
Так как для инвариантных точек λ∙Х = М∙Х , то они являются собственными векторами матрицы преобразования. Собственные значения находятся из характеристического уравнения
det | М –λ ∙Е| = 0.
Матрица коллинеации - третьего порядка, а значит, характеристическое уравнение будет кубическим. При решении кубического уравнения возможны случаи:
· 1 случай. λ1 , λ2 – комплексные, λ3 – действительные корни.
λ3 – дает одну инвариантную точку и в силу принципа двойственности будет одна инвариантная прямая.
· 2 случай. λ1 , λ2 , λ3 – различные действительные корни.
Тогда собственные вектора линейно независимы, а значит, существует три инвариантные точки, причем эти точки различны и не лежат на одной прямой. Эти три точки образуют три неподвижные прямые.
· 3 случай. λ1 = λ2 ≠ λ3 – действительные корни.
Пусть r = rang (М –λ1∙Е), тогда число линейно независимых векторов в подпространстве решений равно 3 – r .
а) λ1 = λ2 - дают один линейно независимый вектор (r = 2). Тогда будет одна инвариантная точка при λ1 и λ3 – даст вторую инвариантную точку. Таким образом, всего две неподвижные точки, которые образуют неподвижную прямую.
б) λ1 = λ2 - дают два линейно независимых вектора, которые образуют двумерное подпространство решений (r = 1), которое в свою очередь порождает точечно неподвижную прямую. λ3 – дает инвариантную точку не принадлежащую точечно неподвижной прямой.
· 4 случай. λ1 = λ2 = λ3 – действительные корни.
а) r = 1  один линейно независимый вектор, а значит одна инвариантная точка;
один линейно независимый вектор, а значит одна инвариантная точка;
б) r = 2  два линейно независимых вектора, а значит две инвариантные точки, которые определяют точечно неподвижную прямую;
два линейно независимых вектора, а значит две инвариантные точки, которые определяют точечно неподвижную прямую;
в) r = 3 - не может быть (почему?).
Собственные вектора находятся из решения системы: (М –λ∙Е)·Х = О
Для нахождения инвариантных прямых характеристическое уравнение будет - det | λ ∙Е – М| = 0, а значит собственные значения те же самые. Собственные вектора находятся из решения системы: и∙(М –λ∙Е) = о.
Задача. Найти инвариантные точки коллинеаций:
а) Уравнение коллинеации 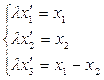
Решение. Матрица коллинеации 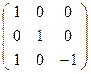 .
.
Характеристическое уравнение: 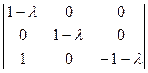 = 0
= 0
 ( 1 - λ)2 ∙(- 1 – λ) = 0,
( 1 - λ)2 ∙(- 1 – λ) = 0,  λ1 = λ2 = 1, λ3 = - 1.
λ1 = λ2 = 1, λ3 = - 1.
При λ1 = 1 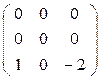 ∙
∙ 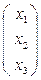 =
= 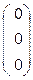

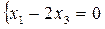
 х1 = 2∙х3 ,
х1 = 2∙х3 ,  М1 =
М1 = 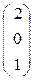 и М2 =
и М2 = 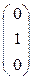 .
.
При λ1 = 1, rang 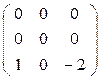 = 1
= 1  коллинеация имеет точечно неподвижную прямую, проходящую через точки М1 и М2 , это прямая - х1 - 2∙х3 = 0.
коллинеация имеет точечно неподвижную прямую, проходящую через точки М1 и М2 , это прямая - х1 - 2∙х3 = 0.
При λ3 = -1 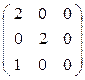 ∙
∙ 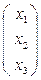 =
= 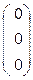

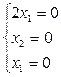
 М3=
М3= 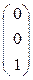 .
.
Кроме того инвариантными будут прямые проходящие через точку М3 и любую точку прямой х1 - 2∙х3 = 0.
det |λ∙Е–М|=0 
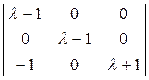 =0
=0  λ1 = λ2 = 1, λ3 = - 1.
λ1 = λ2 = 1, λ3 = - 1.
При λ1 = 1 (и1 : и2 : и3 )∙ 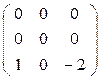 =( 0 : 0 : 0 )
=( 0 : 0 : 0 ) 
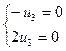
и ( 1 : 0 : 0 ) и v ( 0 : 1 : 0 )  имеем пучок инвариантных прямых (центр пучка - точка М3): λ∙и + μ∙v
имеем пучок инвариантных прямых (центр пучка - точка М3): λ∙и + μ∙v
При λ3 = - 1 ( и1 : и2 : и3 )∙ 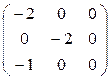 =(0 : 0 : 0 )
=(0 : 0 : 0 ) 
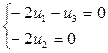
 и ( 1 : 0 : -2 )
и ( 1 : 0 : -2 )  х1 - 2∙х3 = 0 - точечно неподвижная прямая..
х1 - 2∙х3 = 0 - точечно неподвижная прямая..
б) Матрица коллинеации 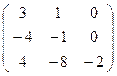 .
.
Решение.
Характеристическое уравнение 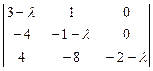 =0
=0
 ( λ2 - 2λ + 1)∙(- 2 – λ) = 0,
( λ2 - 2λ + 1)∙(- 2 – λ) = 0,  λ1 = λ2 = 1, λ3 = - 2.
λ1 = λ2 = 1, λ3 = - 2.
При λ1= 1, 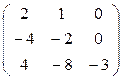 ∙
∙ 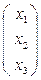 =
= 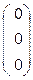

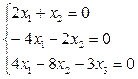

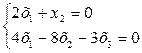
 М1 =
М1 = 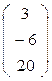 .
.
При λ3 = - 2, 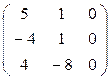 ∙
∙ 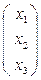 =
= 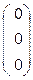

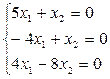
 М3=
М3= 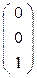 .
.
Задача. Составить уравнение коллинеации, заданной четверками точек
А 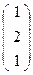 , В
, В 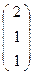 , С
, С  , D
, D 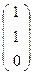 и А′
и А′ 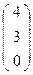 , В′
, В′ 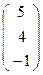 , С′
, С′ 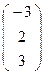 , D′
, D′ 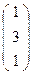 .
.
Решение. Формулы коллинеации имеют вид: λ∙Х ′=A∙Х.
Пусть матрица коллинеации А 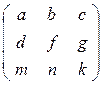 , тогда
, тогда
λ1∙А ′=A∙А → 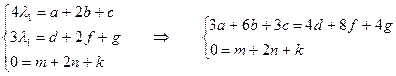 ,
,
λ2∙В ′=A∙В → 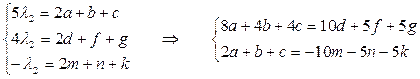 ,
,
λ3∙С′=A∙С → 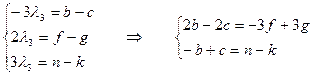 ,
,
λ4∙D ′=A∙D → 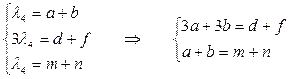 .
.
→ 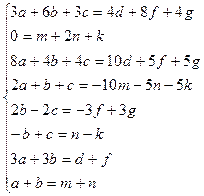 →
→
Одно из решений: а=1, b=0, с=3, d=2, f=1, g= -1, т=0, п=1, k= -2,
тогда А 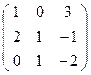 .
.
Гомология
Определение: Не тождественная коллинеация, для которой существует точечно неподвижная прямая называется гомологией.
По принципу двойственности у гомологии будет неподвижная точка.
Определение: Прямая называется осью гомологии. Точка называется центром гомологии.
Обозначение: Р – центр, р – ось.
Определение: Если Р 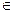 р - гомология называется параболической, если Р
р - гомология называется параболической, если Р 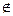 р - гомология называется гиперболической.
р - гомология называется гиперболической.
Теорема. Любая прямая инцидентная центру гомологии является неподвижной.
Доказательство. (самостоятельно).
Свойства:
1. Точка и ее образ лежат на одной прямой с центром 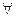 А
А  А′
А′ 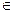 (АР).
(АР).
2. Прямая и ее образ пересекаются на оси 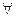 а
а  а′ ∩ а = А0
а′ ∩ а = А0 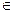 р.
р.

Теорема. Для любых точки Р, прямой р и пары точек А и А′, коллинеарных с точкой Р, существует единственная гомология с центром Р и осью р, переводящая А в А′.
(Сформулируйте теорему двойственную этой.)
Доказательство.
1 случай: Р 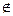 р.
р.
Пусть р ∩(АА′)=Х , возьмем ещё две точки U ≠ V 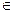 р .
р .
 Рассмотрим две четвёрки точек: А, Р, U, V и А', Р, U, V – в каждой четвёрке точек никакие три не лежат на одной прямой. Тогда можно рассмотреть коллинеацию
Рассмотрим две четвёрки точек: А, Р, U, V и А', Р, U, V – в каждой четвёрке точек никакие три не лежат на одной прямой. Тогда можно рассмотреть коллинеацию
φ: U→U, V→V, Р→Р, А→А′.
Так как U, V – неподвижные точки, тогда неподвижна вся прямая - р, а значит это гомология.
2 случай: Р 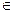 р (самостоятельно). □
р (самостоятельно). □
Вывод: Гомологию можно задать: осью, центром и парой точек, коллинеарных с центром. Гомологию можно задать: осью центром и парой прямых.
Дата добавления: 2022-02-05; просмотров: 1111;











