Нахождение момента силы относительно точки
Пусть в точке А приложена сила F=АВи пусть О – некоторая точка пространства. Из физики известно, что моментом силы Fотносительно точки О называется вектор М, который проходит через точку О и:
перпендикулярен плоскости, проходящей через точки О, А, В;
численно равен произведению силы на плечо;
образует правую тройку векторов.
Стало быть, М = ОА 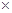 F
F
Смешанное произведение векторов
Уставление компланарности векторов в пространстве
Пример 12: Доказать компланарность векторов 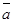 = {1; 1; 3 },
= {1; 1; 3 }, 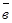 = {0 ; 2 ;- 1 },
= {0 ; 2 ;- 1 }, 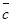 = {1; - 1; 4 }.
= {1; - 1; 4 }.
Решение. Найдем смешанное произведение векторов 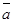
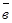
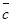 :
:
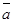
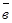
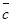 =
= 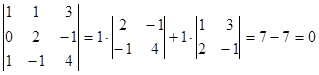 (определитель вычислен путем его разложения по элементам первого столбца).
(определитель вычислен путем его разложения по элементам первого столбца).
Так как смешанное произведение векторов 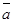 ,
, 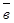 и
и 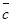 равно нулю, то эти векторы компланарны.
равно нулю, то эти векторы компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Пример 13:Найти объём треугольной пирамиды с вершинами в точках 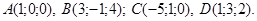
Решение. Найдем координаты векторов 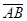 ,
, 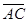 ,
, 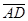 , на которых построена пирамида:
, на которых построена пирамида:
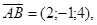
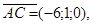
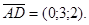
Вычислим смешанное произведение этих векторов
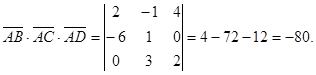
Объём треугольной пирамиды, построенной на векторах 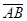 ,
, 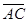 ,
, 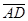 , равен
, равен
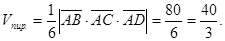
Дата добавления: 2022-02-05; просмотров: 462;











