Векторное пространство, n - мерный вектор
Множество всех плоских или пространственных векторов, рассмотренных ранее нами, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств, в частности 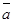 = {Х; У; Z} – вектор в трехмерном пространстве. Очень часто при вычислениях, связанных с векторами отвлекаешься от геометрического смысла вектора и имеешь дело лишь с его координатами. По аналогии с описанной моделью множества векторов трехмерного пространства можно рассмотреть понятие n - мерного векторного пространства.
= {Х; У; Z} – вектор в трехмерном пространстве. Очень часто при вычислениях, связанных с векторами отвлекаешься от геометрического смысла вектора и имеешь дело лишь с его координатами. По аналогии с описанной моделью множества векторов трехмерного пространства можно рассмотреть понятие n - мерного векторного пространства.
Определение: n – мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде 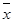 = ( х1, х2, х3, ....., х n )
= ( х1, х2, х3, ....., х n )
Понятие n – мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором 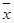 = (х1, х2, х3, ....., х n ), а соответствующие цены – вектором
= (х1, х2, х3, ....., х n ), а соответствующие цены – вектором 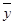 = ( у1, у2 ,у 3,....уn ).
= ( у1, у2 ,у 3,....уn ).
Два n – мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т. е. 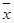 =
= 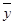 , если хi =уi, i = 1,2,3.....,n.
, если хi =уi, i = 1,2,3.....,n.
Суммой двух векторов одинаковой размерности n называется вектор 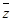 =
= 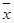 +
+ 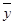 , компоненты которого равны сумме соответствующих компонент слагаемых векторов, т. е . zi = хi + уi i = 1,2,3....., n.
, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т. е . zi = хi + уi i = 1,2,3....., n.
Произведением вектора 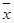 на действительное число l называется вектор
на действительное число l называется вектор 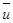 = l
= l  , компоненты ui которого равны произведению l на соответствующие компоненты вектора
, компоненты ui которого равны произведению l на соответствующие компоненты вектора  , т. е. ui = l х i , i = 1, 2, 3....., n.
, т. е. ui = l х i , i = 1, 2, 3....., n.
Линейные операции над любыми векторами удовлетворяют следующимисвойствами:
1.  +
+ 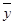 =
= 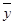 +
+  - коммутативное (переместительное) свойство суммы.
- коммутативное (переместительное) свойство суммы.
2. (  +
+ 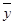 ) +
) + 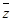 =
=  + (
+ ( 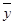 +
+ 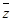 ) – ассоциативное (сочетательное) свойство суммы.
) – ассоциативное (сочетательное) свойство суммы.
3. ( b  ) = (a b )
) = (a b )  - ассоциативное относительно числового множителя свойство.
- ассоциативное относительно числового множителя свойство.
4. (a + b )  = a
= a  + b
+ b  – дистрибутивное (распределительное) относительно суммы числовых множителей свойство.
– дистрибутивное (распределительное) относительно суммы числовых множителей свойство.
5. (  +
+ 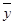 ) = a
) = a  + a
+ a 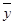 – дистрибутивное относительно суммы векторов свойство.
– дистрибутивное относительно суммы векторов свойство.
6. Существует нулевой вектор 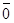 =(0 , 0,.....0) такой, что
=(0 , 0,.....0) такой, что  +
+ 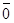 =
=  для любого вектора
для любого вектора  (особая роль нулевого вектора ).
(особая роль нулевого вектора ).
7. Для любого вектора  существует противоположный вектор (-
существует противоположный вектор (-  ) такой, что
) такой, что  +( -
+( -  ) =
) = 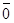 .
.
8. 1 ·  =
=  для любого вектора
для любого вектора  (особая роль числового множителя 1).
(особая роль числового множителя 1).
Определение: Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
По аналогии с линейно зависимыми и линейно независимыми строками матрицы вводится понятие линейной независимости векторов.
Определение: Вектор  m называется линейно комбинацией векторов
m называется линейно комбинацией векторов  1,
1, 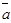 2,
2,  3,....
3,....  m векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:
m векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:  m = l1
m = l1  1+ l2
1+ l2 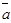 2+ l3
2+ l3  3+....+ l m-1
3+....+ l m-1  m-1 , где l1 , l2 , ... l m-1- произвольные действительные числа.
m-1 , где l1 , l2 , ... l m-1- произвольные действительные числа.
Определение: Векторы  1,
1, 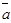 2,
2,  3,....
3,....  m векторного пространства R называются линейно зависимыми, если существуют такие числа l1 , l2 , .....l m , не равные одновременно нулю, что
m векторного пространства R называются линейно зависимыми, если существуют такие числа l1 , l2 , .....l m , не равные одновременно нулю, что
l1  1 + l2
1 + l2 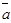 2+ ... +.l m
2+ ... +.l m  m=
m= 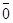 .
.
В противном случае векторы  1,
1, 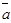 2,
2,  3,....
3,....  m называются линейно независимыми.
m называются линейно независимыми.
Если векторы  1,
1, 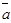 2,
2,  3,....
3,....  m линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
m линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.
Примером линейно независимых векторов являются два неколлинеарных вектора  1 и
1 и 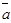 2 на плоскости. Действительно, условие l1
2 на плоскости. Действительно, условие l1  1+ l2
1+ l2 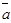 2 = 0 будет выполняться лишь в случае, когда
2 = 0 будет выполняться лишь в случае, когда
l1= l2 = 0, ибо если, например l2 ¹ 0, то 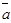 2 = –
2 = – 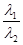
 1 и векторы
1 и векторы  1 и
1 и 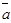 2 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
2 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Свойства векторов линейного пространства:
1. Если среди векторов  1,
1, 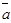 2,
2,  3,....
3,....  m имеется нулевой, то эти векторы линейно зависимы.
m имеется нулевой, то эти векторы линейно зависимы.
2. Если часть векторов  1,
1, 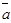 2,
2, 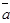 3,....
3,....  m являются линейно зависимыми, то и все эти векторы – линейно зависимые.
m являются линейно зависимыми, то и все эти векторы – линейно зависимые.
Действительно, если, например, векторы  1,
1, 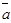 2,
2,  3,....
3,....  m линейно зависимы, то справедливо равенство l2
m линейно зависимы, то справедливо равенство l2 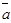 2 + l m
2 + l m  m=
m= 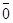 , в котором не все числа l2.... l m и l1= 0 будет справедливо равенство l1
, в котором не все числа l2.... l m и l1= 0 будет справедливо равенство l1  1 + l2
1 + l2 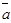 2+ ... +.l m
2+ ... +.l m  m=
m= 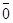 .
.
Пример: Выяснить, являются ли векторы  1 =(1, 3, 1, 3),
1 =(1, 3, 1, 3), 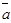 2 = (2, 1, 1, 2 ),
2 = (2, 1, 1, 2 ),  3 = ( 3, - 1, 1, 1 ) линейно зависимыми.
3 = ( 3, - 1, 1, 1 ) линейно зависимыми.
Решение. Составим векторное равенство l1  1 + l2
1 + l2 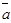 2+l3
2+l3  3 =
3 = 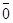 или
или
l1 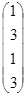 + l2
+ l2 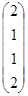 + l3
+ l3 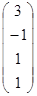 =
= 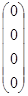 .
.
Задача свелась, таким образом, к решению системы:
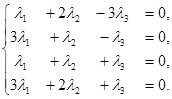 Решая систему методом Гаусса, приведем ее к виду:
Решая систему методом Гаусса, приведем ее к виду:
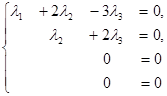 откуда найдем бесконечное множество ее решений (l1 = с, l2 = -2с, l3 = с), где с - произвольное действительное число.
откуда найдем бесконечное множество ее решений (l1 = с, l2 = -2с, l3 = с), где с - произвольное действительное число.
Итак, для данных векторов условие l1  1 + l2
1 + l2 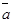 2+ ... +.l m
2+ ... +.l m  m=
m= 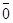 выполняется не толдько при l1 = l2 = l3 =0 (а, например, при l1=1, l2 = -2, l3 =1 (с =1); при l1 =2, l2 =-4, l3 =2 (с =2) и т.д.), следовательно, эти векторы – линейно зависимые.
выполняется не толдько при l1 = l2 = l3 =0 (а, например, при l1=1, l2 = -2, l3 =1 (с =1); при l1 =2, l2 =-4, l3 =2 (с =2) и т.д.), следовательно, эти векторы – линейно зависимые.
Линейное пространство R называется n- мерным, если в нем существует n линейно независимым вектором, а любые из (n + 1) векторов уже являются зависимыми. Другими словами, размерность пространства - это максимальное число содержащихся в нем линейно независимых векторов. Число n называется размерностью пространства R и обозначает dim(R) .
Совокупность n линейно независимых векторов n- мерного пространства R называется базисом.
Теорема: Каждый вектор хлинейного пространства R можно представить и притом единственным способом в виде линейной комбинации векторов базиса.
Доказательство:
Пусть векторы е1, е2 ,..., еn образуют произвольный базис n- мерного пространства R . Так как любые из
(n + 1) векторов n- мерного пространства R зависимы , то будут зависимы , в частности , векторы е1 , е2,..., еn и рассматриваемый вектор х. Тогда существуют такие не равные одновременно нулю числа l1, l2 ,ln , l , что
l1 е1 + l2 е2 +...+ l n еn + lх=0
При этом l ¹ 0, ибо в противном случае , если l = 0 и хотя бы одно из чисел l1, l2 ,..., ln было бы
отлично от нуля, то векторы е1 , е2 ,..., еn были бы линейно зависимы. Следовательно,
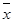 = -
= - 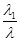 е1 -
е1 - 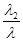 е2 - ... -
е2 - ... - 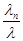 еn или
еn или 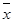 = х1е1 +х2 е2 +...+х nеn где х i = -
= х1е1 +х2 е2 +...+х nеn где х i = - 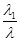 (i = 1, 2, ...., n) (*)
(i = 1, 2, ...., n) (*)
Это выражение 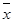 через е1, е2,..., еn единственное, так как если допустить какое – либо другое выражение, например,
через е1, е2,..., еn единственное, так как если допустить какое – либо другое выражение, например, 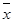 = у1е1 +у2 е2 +...+у nеn , то, вычитая из него почленно ( * ), получим
= у1е1 +у2 е2 +...+у nеn , то, вычитая из него почленно ( * ), получим
( у1 – х 1) е1 + (у2 – х 2) е2 + ...+ (у n – х n) еn = 0 , откуда из условия линейной независимости векторов е1 , е2,..., еn следует, что у1 – х 1= у2 – х 2= ...= у n – х n = 0 или у1 = х 1, у2 = х 2 ... у n = х n у n = х n . g
Равенство ( * ) называется разложением вектора 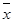 по базису е1 , е2,..., еn, а числа х 1, х 2 ... х n – координаты вектора
по базису е1 , е2,..., еn, а числа х 1, х 2 ... х n – координаты вектора 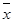 относительно этого базиса. В силу единственности этого разложения каждый вектор однозначно может быть определен координатами в некотором базисе.
относительно этого базиса. В силу единственности этого разложения каждый вектор однозначно может быть определен координатами в некотором базисе.
Важное значение имеет следующая теорема, которую мы приведем без доказательства:
Теорема. Если е1 , е2,..., еn – система линейно независимых векторов пространства R и любой вектор алинейно выражается через е1 , е2,..., еn ,то пространство R является n- мерным , а векторы е1 , е2,..., еn – его базисом.
Пример.В базисе е1, е2 , е3 заданы векторы а1 = (1; 1; 0), а2= (1; -1; 1) и а3 = (-3; 5;-6) . Показать, что векторы а1 ,а2 , а3 образуют базис.
Решение.Векторы а1 , а2 , а3 образуют базис, если они линейно независимы. Составим векторное равенство: l1 а1+ l2 а2 + l 3 а 3 = 0. Решая его аналогично примеру 1 можно убедиться в единственном нулевом решении: l1 + l2 + l 3 = 0 , т.е. векторы а1 , а2 , а3 образуют систему линейно независимых векторов и, следовательно, составляют базис.
Дата добавления: 2022-02-05; просмотров: 1008;











