Векторы в экономике

Следует отметить, что под , , 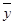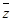можно рассматривать не только векторы, но и элементы любой природы. В этом случае соответствующее множество элементов называется линейным пространством.

Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент.

Экономическая иллюстрация n-мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров n; количества каждого из них, приобретенные потребителем, характеризуются набором товаров x = (x₁, x₂, ..., x_n), где через x_i обозначается количество i-го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров C = {x = (x₁, x₂, ... , x_n) x_i ³ 0, i = 0, 1, 2,…n}. В дальнейшем предполагаем, что каждый товар имеет цену. Все цены предполагаются строго положительными. Пусть цена единицы i-го товара есть pi, тогда вектор Р = (p1, ..., pn) есть вектор цен. Набор товаров, как вектор, имеет ту же размерность, что и век-тор цен. Для набора товаров X = (xi) и вектора цен P = (pi) их скалярное произведение P X = p1x1 +... + pnxn есть число, называемое ценой

набора или его стоимостью, и будет обозначаться c(X).

Пример 1:

1. В районе три обменных пункта валюты от одного банка. Об-

мен в них идет только долларов и евро на рубли. Каждый вечер остаток всех денег сдается в банк. Обозначим через Mi вектор денежных средств, сдаваемых i-м пунктом. Имеют ли смысл (и какой именно) векторы M1 + M2, M1 + M2 + M3?

Решение ясно. Но далеко не всегда сложение векторов имеет ясный содержательный смысл. В приведенной задаче такой смысл есть. Но если трехмерный вектор есть (размер бюста, окружность талии, объем бедер), то трудно придать какой-нибудь содержательный смысл сложению таких векторов.

Пример 2: Пусть завод производит мужские, женские и детские велосипеды. Тогда объем его производства V за год можно записать как вектор (M, L, D), где M — объем производства за год мужских велосипедов, L — женских и D — детских. Например, пусть объем производства в 2006 г. был 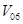= (1000, 800, 4000). Предположим, что план на 2007 г. на 10% больше объема производства в 2006 г., тогда этот план есть вектор 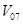= (1100, 880, 4400). Пусть торговая фирма ≪Велосипеды≫ покупает половину всей продукции завода, тогда в 2006 г. она купила W = (500, 400, 2000). Предположим, что в стране всего три велосипедных завода, объемы производства которых в 2006 г. были Q 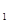= (1000, 800, 4000), Q 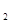= (1000, 600, 2000), Q 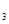= (2000,1600, 8000). Тогда все три завода вместе произвели Q = (4000, 3000, 14 000), т.е. 4000 мужских, 3000 женских и 14 000 детских велосипедов. 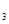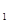Можно также отметить, что Q = 2 Q , т.е. 3-й завод произвел в 2 раза больше велосипедов каждого вида, чем 1-й завод. Приведенные выше векторы 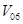, , 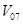W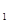, Q 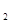, Q , Q 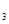и т.д. — это примеры конкретных векторов. Произвольный трехмерный вектор можно обозначить 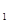(x 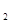, x , x 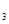) или кратко X.