Задачи для самостоятельной работы
1. По данным векторам а и b построить следующие их линейные комбинации: а) 2а + b; б) а — Зb; в) — а + 4-b;
2. Векторы 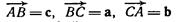 служат сторонами треугольника ABC. Выразить через а, b, с векторы
служат сторонами треугольника ABC. Выразить через а, b, с векторы 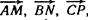 совпадающие с медианами треугольника.
совпадающие с медианами треугольника.
3. В треугольной пирамиде SABC известны векторы Найти вектор 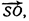 , если точка О является центром масс
, если точка О является центром масс 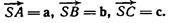 треугольника ABC.
треугольника ABC.
4. Дана прямоугольная трапеция ABCD, длины оснований AD н ВС которой соответственно равны 4 и 2, а угол D равен 45°. Найти проекции векторов  на ось
на ось 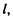 определяемую вектором
определяемую вектором 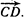 .
.
5. Вектор а составляет с координатными осямн Ох и Оу углы 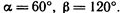 . Вычислить его координаты, если |а| =2.
. Вычислить его координаты, если |а| =2.
6. Найти длины диагоналей параллелограмма, построенного на векторах 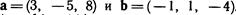
7. Векторы  определяют стороны треугольника ABC. Найти длину вектора
определяют стороны треугольника ABC. Найти длину вектора  , совпадающего с медианой, проведенной из вершины С.
, совпадающего с медианой, проведенной из вершины С.
8.В параллелограмме ABCD даны стороны 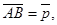

Выразить через 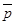 и
и 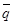 векторы
векторы 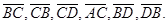
9. В Треугольнике ABC проведины меридианы a AK, BL и CM. Выразить 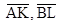 и
и 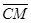 через векторы
через векторы 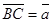 и
и 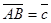 .
.
10. Даны векторы 
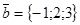 и
и  . Найти векторы:
. Найти векторы:  ;
; 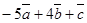 .
.
11. Найти направляющие косинусы вектора 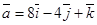
12.Дано 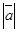 =5,
=5,  =6. Найти скалярное произведение векторов
=6. Найти скалярное произведение векторов 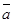 и
и 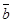 , если угол
, если угол  между ними равен 120°
между ними равен 120°
13. Найти угол А в треугольнике с вершинами A(1;2;-1), B(5;5;11), C(13;18;20)
14. Даны векторы 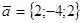 ,
, 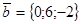 ,
, 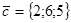 . Найти проекцию вектора
. Найти проекцию вектора 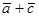 на вектор
на вектор 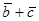 .
.
15. Даны векторы 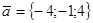 ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора 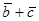 на вектор
на вектор  .
.
16. Найти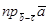 ,если
,если 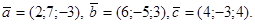
17. Даны векторы 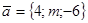 и
и 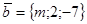 . При каком значении m эти векторы перпендикулярны?
. При каком значении m эти векторы перпендикулярны?
18.Даны три последовательные вершины параллелограмма А (-3;-2;0), В(3;-3;1) и С(5;0;2). Найти четвёртую вершину D и угол между векторами 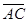 и
и 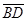 .
.
19. Даны векторы 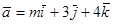 и
и 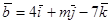 . При каком значении m векторы перпендикулярны?
. При каком значении m векторы перпендикулярны?
20. Найти площадь треугольника с вершинами А (2;2;2), В(1;3;3), С(3;4;2).
21. Упростить: 
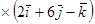
22. Известно, что 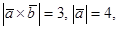 а угол между
а угол между 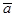 и
и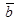 равен
равен  Найти
Найти 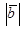 .
.
23. Найти площадь треугольника с вершинами в точках 

24. Вычислить площадь треугольника с вершинами А (1;1;1), В (2;3;4), С (4;3;2).
25. Вычислить площадь и высоту параллелограмма, построенного на векторах 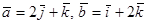
26. Найти площадь параллелограмма, построенного на векторах 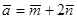 и
и 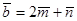 , где
, где 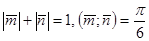 .
.
27. Вычислить диагонали и площадь параллелограмма, построенного на векторах  и
и  .
.
28. Найти значения α и β, при которых векторы 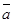 =
=  и
и 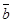 =
= 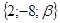 являются коллинеарными.
являются коллинеарными.
29. На оси аппликат найти точку, равноудаленную от точек А(3;9;-1) и В(7;-3;9)
30. Определите координаты концов P и Q отрезка, который точками М(3;1;3) и N(6;-1;1) разделён на три части.
31. Проверить, является ли векторы 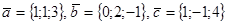 компланарными?
компланарными?
32. Найти объём тетраэдра с вершинами в точках А (-1;1;0), В(2;-2;1), С(3;1;-1), D(1;0;-2).
33. Вычислить объём параллелепипеда, построенного на векторах 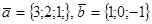 и
и  .
.
34. Установить, лежат ли в одной плоскости точки А (4;3;10), В (5;1;5), С (2;2;5), D (3;4;12).
35. В тетраэдре с вершинами D (-3;-3;-3), A (2;-1;-3), B (-1;2;3) и
C(-2;-2;1). Найти площадь грани АВС и длину высоты, проведённой к этой грани.
36.Выяснить, компланарны ли векторы 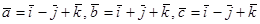 ?
?
34. Определить 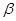 , при котором компланарны векторы
, при котором компланарны векторы 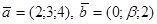 и
и 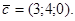
37. Найти объем тетраэдра с вершинами в точках А (-1; 1; 0 ), В ( 2; -2; 1 ), С (3; 1; -1 ), D =(1; 0; -2 ).
38. На прямой проходящей через точки А (-3;8;2) и B (1;-2;0) найти точку С, абсцисса которой 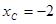
39. Найти объём треугольной пирамиды с вершинами в точках 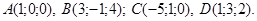
40. Найти точку пересечения медиан треугольника, если вершинами его служат точки А(7;-4;5), В(-1;8;-2), С(-12;-1;6).
41. Найти все значения m, при которых вектор а(1; m; 3) линейно выражается через векторы b (2;3;7), c (3;-2;4), d (-1;1;-1).
42. Предприятие выпускает 4 вида продукции Р1, Р2; Р3, Р4 в количествах 50, 80, 20,120 единиц. При этом нормы расхода сырья составляют соответственно 7; 3,5; 10; 4 кг. Определите суммарный расход сырья и его изменение при изменениях выпуска продукции Р1, Р2; Р3, Р4 соответственно +5, -4, -2, +10 единиц.
43. Предприятие выпускает три вида продукции Р1, Р2; Р3 в количестве 15, 25, 40 штук, реализуемых по ценам 30, 40, 50 усл. Ед. соответственно. Найти выручку предприятия от реализации продукции и ее изменение при изменении Р1, Р2; Р3цен продукции соответственно на +5, -3, +2 усл. ед.
44. Выяснить, являются ли векторы а1=(4;-5;2;6),а2=(2;-2;1;3),а3=(6;-3;3;9),а4=(4; -1;5;6) линейно зависимыми?
3. Ответы:
4. 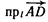
 ,
,
5. 
6. 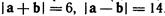 7.
7. 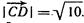
8. 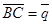 ,
, 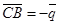 ,
, 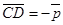 ,
, 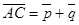 ,
, 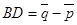
 ;
;
9.  ,
, 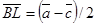 ,
, 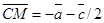 ;
;
10 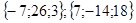 ; 11. cos
; 11. cos 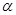 =8/9,cos
=8/9,cos  =-4/9,cos
=-4/9,cos 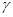 =1/9; 12. -15; 13.
=1/9; 12. -15; 13. 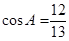 ; 14.
; 14. 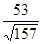 ; 15. 14/11; 16. -7/3; 17. -7; 18. D(-1;1;1)
; 15. 14/11; 16. -7/3; 17. -7; 18. D(-1;1;1)  ; 19. 4; 20.
; 19. 4; 20.  /2, 22.
/2, 22. 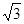 /2; 23.
/2; 23.  ; 24.
; 24. 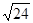 ; 25.
; 25. 
 /
/ 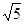 , 28. α=12; β=-6, 29. (0;0;12/5); 30. P(0;3;5) Q(9;-3;-1); 34. 1/6;
, 28. α=12; β=-6, 29. (0;0;12/5); 30. P(0;3;5) Q(9;-3;-1); 34. 1/6;
35. С(-2; 11/2; 3/2); 37. 25/6; 39.40/3; 40.(-2;1;3); 41. 1; 42. 1310 кг.; 41 кг.; 43. 3450 усл. ед.; 80 усл. ед.
Дата добавления: 2022-02-05; просмотров: 474;











