Дискретное позиционное управление отдельным приводом

Основной вариант алгоритма дискретного позиционного программного управления приводом соответствует структурной схеме следящей систе­мы (см. рис. 4.1), которая последовательно отрабатывает заданные при­ращения управляемой выходной координаты q_i. Эта схема может быть дополнена другими средствами коррекции, компенсирующими воздейст­вия внешних возмущений и, прежде всего, нагрузки, торможением в точ­ках позиционирования с помощью специального тормоза.

Синтез оптимального алгоритма управления при необходимости обеспе­чить максимальное быстродействие, как уже отмечалось в главе 6, приво­дит к релейному управлению. Однако поскольку такая система двухпозиционного релейного управления неустойчива в малом, при подходе к точкам позиционирования необходимо переходить на другой алгоритм управления. В результате получается система так называемого дуального управления с переменной структурой, показанная на рис. 7.2. Устройство управления непрерывного действия включается вблизи очередной точки

позиционирования, т. е. при малом рассогласовании Δq = q - q₃ > а уст­ройство релейного управления включается в момент подачи программ­ного задания на очередной шаг и также при возникновении больших рассогласований, вызванных любыми причинами.. (Коммутирующий элемент КЭ на рис. 7.2 показан условно. Такой же алгоритм может быть реализован, например, с помощью управляемых ключей, осуществляю­щих нужного знака форсировку двигателя в соответствующие интервалы времени.)

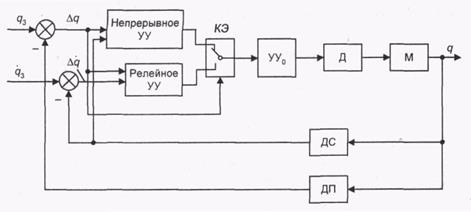
Рис. 7.2. Схема системы дуального управления приводом: КЭ — коммутирующий элемент

Рассмотрим алгоритмы релейного управления, а затем вернемся к каналу непрерывного управления. На рис. 7.3 показан процесс такого опти­мального по быстродействию релейного управления электрическим при­водом, описываемый 2 дифференциальными уравнениями первого по­рядка с ограничениями по входному напряжению и по движущему моменту, т. е. по току [23].

В соответствии с теорией оптимального управления оптимальный алго­ритм процесса управления напряжением на входе привода состоит из 3 интервалов: на первом из которых предельное значение имеет момент двигателя М_д=М_дпр, на втором — напряжение на его входе (на якоре) u=u_пр и на третьем — опять М_д, но уже с обратным знаком М_д=-М_{д пр}.

На рис. 7.3, а на фазовой плоскости сплошными линиями показаны оп­тимальные по быстродействию процессы движения при отработке зада­ния ф₃ при ограничении по движущему моменту М_д=С_м1. Они состоят из парабол, выходящих из начальных точек (φ₃,0) на оси абсцисс, и общей параболы, описывающей этап торможения, — линии переключения. (Пунктиром показан процесс, соответствующий наличию ограничения еще и скорости. Напомним, что момент и скорость связаны механиче­ской характеристикой двигателя.)

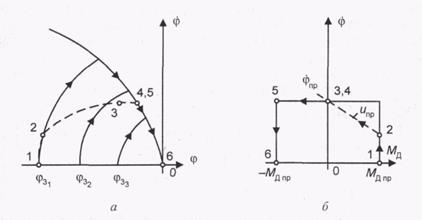
Рис. 7.3. Фазовые траектории (а) и механические характеристики (б) электропривода с релейным позиционным управлением: φ — угол поворота выходного вала двигателя; М_д— движущий момент; u_пр — предельное значение напряжения на входе двигателя

Для двигателя постоянного тока с независимым возбуждением и управ­лением по напряжению на якоре ограниченные переменные связаны с напряжением на якоре известными выражениями:

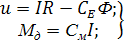(7.1)

Здесь I — ток в цепи якоря двигателя, имеющий ограничение 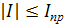, которое определяет предельное значение момента М_д≤М_дпр =С_мI_пр, где С_м — коэффициент электромагнитного момента;С_Е — коэффициент противо-э.д.с. двигателя, R — активное сопротивление цепи якоря дви­гателя.

Уравнение линии переключения выглядит так:

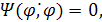
где 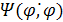— функция переключения.

Для RI_пр≤u_пр

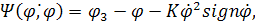(7.2)

где 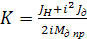, i — передаточное отношение редуктора привода, а J_H и J_д—моменты инерции нагрузки и якоря двигателя.

Алгоритм управления двигателем представляет собой двухпозиционное релейное управление с входным сигналом ±u_пр. Знак этого сигнала оп­ределяется знаком функции переключения (7.2). Ограничение тока при этом осуществляется с помощью обратной связи по току. При достаточ­но сильной этой связи ток, а, следовательно, и момент двигателя будут практически безинерционно следовать за входным напряжением и, реа­лизуя режим моментного управления двигателем.

Отрезок 1—2 на рис. 7.3 соответствует этапу разгона с постоянным уско­рением, т. е. с М_д=М_{д пр}; участок 2—3 — продолжение этапа разгона, но с и = u_пр, когда с ростом противо-э.д.с. напряжение на якоре достигло своего предельного значения; 3—4 — этап движения с постоянной скоро­стью, который может возникать при достаточно большой длительности процесса разгона в прежнем режиме ограничения и; 4—5 — момент пере­хода к этапу торможения реверсированием тока якоря и соответственно момента; 5—6 — этап торможения при M_д= - M_{д пр}.