Математическое описание манипулятора с приводами

В общем виде математическое описание манипулятора включает рас­смотренные зависимости:

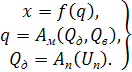(5.29)

Здесь Ами Ап — операторы механической системы и системы приво­дов манипулятора, а Uп— вектор управляющих воздействий на входе приводов.

Если воспользоваться уравнением динамики манипулятора (5.14) и ли­неаризовать уравнение привода по схеме на рис. 4.1, получим структур­ную схему манипулятора с такими приводами, показанную на рис. 5.8, и систему уравнений:

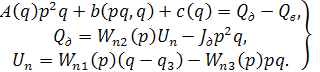(5.30)

Здесь Uп — вектор управляющих воздействий на входе системы приво­дов; W_n2(р) — передаточная матрица системы приводов, связывающая векторы (Qд ^и Uп; W_n1(р); W_n3(р) — передаточные матрицы последователь­ных и параллельных корректирующих звеньев, J_д— диагональная мат­рица моментов инерции двигателей, приведенных к выходу приводов q (умножением на квадрат передаточного отношения редуктора).

Исключив в (5.30) промежуточные переменные можно получить следую­щее общее уравнение:

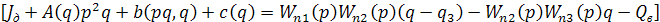
(5.31)

При необходимости в схему, приведенную на рис.5.8, могут быть введены различные нелинейности типа насыщения, нечувствительности, сухого трения и т. п.

Вместе с тем при исследовании конкретных систем и конкретных режимов их работы в их математическом описании могут быть сделаны и следующие упрощения.

1. При невысоких скоростях движения (примерно менее 0,5 м/с), когда динамическое взаимовлияние приводов мало, можно пренебречь этим взаимовлиянием по ускорению и скорости, т. е. недиагональными элементами матрицы А(q) и смешанными произведениями скоростей в выражении b(pq,q) [17].

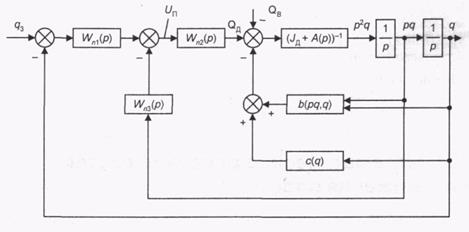
Рис. 5.8. Структурная схема манипулятора с приводами

В этом случае левая часть уравнения (5.31) принимает вид:

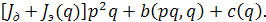
Здесь 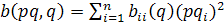, т.е. не содержит членов ;

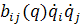Jэ(q)=(J_1э,J_2э,…J_nэ) – диагональная матрица эффективных моментов инерции относительно q_i i-го и всех последующих звеньев (i+1),...,п, которая находится по формуле:

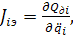(5.32)

т. е. исходя из уравнения динамики механической системы манипуля­тора при замене А(q) на J_э(q). Соответственно это выражение можно представить так:

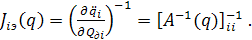(5.33)

Кроме того, при наличии в приводах редукторов с большим переда­точным числом величинами J_дi(q можно пренебречь по сравнению с J_дi и соответственно в уравнении (5.31) пренебречь А(q).

2. Обычно, особенно при невысоких скоростях движения, переходные
процессы в приводах протекают существенно быстрее, чем перемеще­ния самого манипулятора. Поэтому уравнение манипулятора (5.31) можно разделить на 2 решаемых независимо: одно уравнение в виде уравнения (5.31) при p =0 в его правой части и второе в виде второго и третьего уравнений системы (5.30).

3. Можно, используя метод "замороженных" коэффициентов, разбить рабочую зону манипулятора на участки, в которых в членах b(pq,q) и с(q) уравнения динамики манипулятора ставить постоянные значения q.