Аксиомы (тождества) алгебры логики

а) аксиомы операции отрицания:

_

0 = 1 или дуальное отношение ;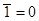

б) аксиомы операций с константами 0 и 1:

0 Ù 0 = 0 или 1 Ú 1 = 1;

1 Ù 0 = 0 Ù1 = 0 или 0 Ú 1 = 1 Ú 0 = 1;

1 Ù 1 = 1 или 0 Ú 0 = 0.

Из аксиом вытекают законы булевой алгебры.

а) Переместительный закон (закон коммутативности):

Х₁ Ù Х₂ = Х₂ Ù Х₁ или Х₁ Ú Х₂ = Х₂ Ú Х₁.

б) Сочетательный закон (закон ассоциативности):

Х₁ Ù Х₂ Ù Х₃ = Х₁ Ù (Х₂ Ù Х₃) = (Х₁ Ù Х₂) Ù Х₃ или

Х₁ Ú Х₂ Ú Х₃ = Х₁ Ú (Х₂ Ú Х₃) = (Х₁ Ú Х₂) Ú Х₃.

в) Распределительный закон ( закон дистрибутивности):

Х₁ Ù (Х₂ Ú Х₃) = Х₁ Ù Х₂ Ú Х₁ Ù Х₃ или

Х₁ Ú (Х₂ Ù Х₃) = Х₁ Ú Х₂ Ù Х₁Ú Х₃.

г) Закон повторения (тавтологии, идемпотентности):

Х₁ Ù Х₁ Ù Х₁= Х₁ или Х₁ Ú Х₁ Ú Х₁ = Х₁.

д) Законы операций с константами:

Х₁ Ù 0 = 0 или Х₁ Ú 1 = 1;

Х₁ Ù 1 = Х₁ или Х₁ Ú 0 = Х₁.

е) Закон двойной инверсии:

Х = Х.

ж) Закон обращения:

__ __

если Х₁ = Х₂ , то Х₁ = Х₂.

з) Закон дополнительности:

__ __

Х₁ Ù Х₁ =0 или Х₁ Ú Х₁ = 1.

и) Законы дуальности (законы де Моргана):

_______________ ___ __ __

Х₁ Ù Х₂ Ù .... Ù Хn = Х₁ Ú Х₂ Ú ..... Ú Хn.

Инверсия конъюнкции (логического произведения) двух и более переменных равна дизъюнкции (логической сумме) инверсий этих переменных.

_______________ __ __ ___

Х₁ Ú Х₂ Ú .... Ú Хn = Х₁ Ù Х₂ Ù .... Ù Хn.

Инверсия дизъюнкции (логической суммы) двух и более переменных равна конъюнкции (логическому произведению) инверсий этих переменных.

к) Закон (правило) поглощения:

Х₁ Ú (Х₁ Ù Х₂) = Х₁ или Х₁ Ù ( Х₁ Ú Х₂) = Х₁.

Поглощается переменная Х₂.

л) Закон (правило) склеивания:

__

( Х₁ Ù Х₂ ) Ú ( Х₁ Ù Х₂ ) = Х₁ или дуальная форма

__

( Х₁ Ú Х₂ ) Ù ( Х₁ Ú X₂ ) = Х₁.

м) Правило вычеркивания:

__ __

(Х₁ Ù Х₂ ) Ú Х₁ = Х₂ Ú Х₁ или дуальная форма

___ ___

(Х₁ Ú Х₂ ) Ù Х₁ = Х₂ Ù Х₁.

Задание.

Используя полученные ранее выводы о соответствии логических уравнений и релейно-контактных схем, сопоставьте логическим уравнениям рассмотренных законов релейную схему и проанализируйте ее работу.