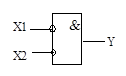Основные логические функции
БУЛЕВА АЛГЕБРА И ЕЕ ОСНОВНЫЕ ЗАКОНЫ
Математический аппарат, описывающий работу дискретных устройств, базируется на алгебре логики, или как ее называют по имени одного из создателей - английского математика Дж. Буля (1815 - 1864 гг.) - на булевой алгебре.
Слово ”логика” означает систематический метод рассуждений. Логика базируется на исчислении высказываний, что представляет собой совокупность правил для определения истинности или ложности некоторой комбинации высказываний [ 1 ].
Именно на анализ рассуждений и была ориентирована алгебра, описанная Дж. Булем, но в 1910 г. П.С. Эренфест впервые применил булеву алгебру для анализа контактных цепей, чем положил начало широкому использованию булевой алгебры в технике.
Основные логические функции
Возьмем в качестве аналога логической функции электрическую цепь с контактами. Обозначим наличие входного сигнала управления контактом Х=1, а его отсутствие Х=0. Если в результате действия входного сигнала цепь замкнется, будем считать выходной сигнал Y= 1, если цепь будет разомкнута, то Y=0. В современной технике контактные элементы заменяют бесконтактными (например, на тиристоры или транзисторы в ключевом режиме). Два значения логических сигналов в этом случае физически представляются в виде двух уровней электрического напряжения: низкого и высокого.
а) Рассмотрим цепь с одним замыкающим контактом (рис.1).
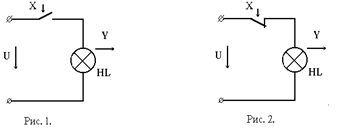
Логику ее работы можно записать следующим образом:
“Если Х= 0, то Y= 0. Если Х= 1, то и Y= 1”;
Для сокращения записей анализ связей входных и выходных сигналов оформляется в виде таблицы, называемой таблицей состояния или таблицей истинности. Эта таблица имеет (m+ n ) столбцов и 2n строк, где n — число входных переменных (сигналов), а m — число выходных сигналов.
| Х | Y |
Мы имеем 1 входной сигнал и 1 выходной сигналы, следовательно, таблица состояний имеет два столбца и две строки. Выходной сигнал Y повторяет значение входного сигнала Х.
Такая функция называется функцией повторения.
|
 Уравнение: Y = X.
Уравнение: Y = X.
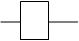
б) Рассмотрим цепь с размыкающим контактом (рис. 2). Если нет воздействия на контакт цепи, то цепь замкнута, иначе цепь размыкается.
Логика работы может быть словесно описана следующим образом:
“ Если Х НЕ 1, то Y = 1 ”.
| Х | Y |
Выходной сигнал имеет значение, противоположное (инверсное) входному. Такая логическая функция получила название функции отрицания, или функции инверсии, или функции НЕ.
__
 Уравнение: Y = Х(читается Y НЕ Х).
Уравнение: Y = Х(читается Y НЕ Х).
 Черта над переменной обозначает инверсию сигнала.
Черта над переменной обозначает инверсию сигнала.
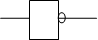 Графическое обозначение элемента НЕ:
Графическое обозначение элемента НЕ:
Кружок на выходе обозначает инверсию
выходного сигнала.
Рис.4. Обозначение элемента НЕ.
Рассмотрим далее логические функции двух переменных, что соответствует электрической цепи с двумя контактами.
в) Цепь с последовательно соединенными замыкающими контактами. 
Схема Таблица истинности
| Х1 | Х2 | Y |
Х1 ¯ Х2 ¯ ®Y
 |
Рис. 5.
Словесная формулировка алгоритма работы схемы:
“ Если Х1 = 1 И Х2 = 1, то У = 1”.
Логическая функция получила название функции И, или функциилогического умножения (конъюнкции).
Уравнение функции: Y = Х1 Ù Х2 (читается: “ Y равно Х1 И Х2“),
где Ù - символ операции конъюнкции.
Допускается использовать знак обычного умножения ( × ). Y = Х1 × Х2.
Графическое обозначение Х1
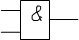 логического элемента И : Y
логического элемента И : Y
Знак & - символ логической операции И. Х2
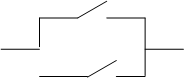
г) Цепь с параллельно соединенными замыкающими контактами.
Схема Таблица истинности
| Х1 | Х2 | Y |
| Х1 | Х2 | Y |
 Х1 ¯
Х1 ¯
®Y

 Х2 ¯
Х2 ¯
 |
Рис.6.
Словесное описание работы схемы:
“Если Х1 = 1, ИЛИ Х2 = 1, ИЛИ оба равны 1, то Y = 1”.
Эта логическая функция получила название функции ИЛИ, функциилогического сложения (дизъюнкции).
Уравнение функции: Y = Х1 Ú Х2 (читается : Y равно Х1 ИЛИ Х2),
где Ú — символ операции дизъюнкции.
Допускается использовать знак обычного сложения “+” с учетом понимания из контекста, что речь идет о логическом сложении.
Y = Х1 + Х2.
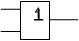 Х1
Х1
Графическое обозначение элемента ИЛИ: Y
Х2
д) Цепь с последовательно включенными размыкающими контактами.
Схема Таблица истинности
| Х1 | Х2 | Y |
Х1 ¯ Х2 ¯ Y®
 |
Рис.7.
Описание работы схемы:
“ Если Х1 = 1 ИЛИ Х2 = 1, то YНЕ 1”.
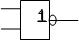 Это логическая функция ИЛИ-НЕ. Она имеет специальное название - стрелка Пирса. _______ Х1
Это логическая функция ИЛИ-НЕ. Она имеет специальное название - стрелка Пирса. _______ Х1
Уравнение функции: Y = Х1 Ú Х2 . Обозначение: Y
Х2
Сначала производится логическая операция ИЛИ над входными сигналами, а затем операция НЕ (инверсия) над результатом.
Проанализировав таблицу состояний элемента ИЛИ-НЕ, его работу можно описать другим способом:
“ Если Х1 НЕ 1 И Х2 НЕ 1, то Y = 1”.
Здесь сначала входные сигналы инвертируются, а затем производится операция И.
|
Это соответствует уравнению:
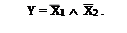
Из рассмотренного примера следует интересная формула, которую в дальнейшем мы встретим в виде закона или правила Де Моргана:
________ ___ ___
Y = Х1 Ú Х2 = Х1 Ù Х2.
е) Цепь с параллельно включенными размыкающими контактами
Схема Таблица истинности
Х1 ¯
| Х1 | Х2 | Y |
® Y
Х2 ¯
Рис.8.
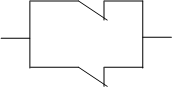
Описание работы схемы:
“Если Х1 = 1 И Х2 = 1 , то Y НЕ 1 “.
Цепь разомкнута только тогда, когда разомкнуты оба контакта.
Это логическая функция И-НЕ, или функция Шеффера.
_______
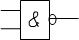 Логическое уравнение: Y = Х1 Ù Х2. Х1 Y
Логическое уравнение: Y = Х1 Ù Х2. Х1 Y
Условное графическое обозначение (УГО): Х2
Аналогично предыдущему логику работы схемы можно описать по-другому:
“ Если Х1 НЕ 1 ИЛИ Х2 НЕ 1, то Y = 1”.
 Это будет соответствовать уравнению:
Это будет соответствовать уравнению:
Y = Х1 Ú Х2 = Х1 Ù Х2.
Далее рассмотрим несколько цепей, содержащих и замыкающие, и размыкающие контакты двух переменных.
ж) Цепь с последовательно включенными замыкающим и размыкающим контактами.
Схема Таблица истинности
| Х1 | Х2 | Y |
| Х1 | Х2 | Y |
Х1 ¯ Х2 ¯
 Y®
Y®
Рис.9.
Выходной сигнал Y повторяет входной сигнал Х1, если нет сигнала Х2, иначе выходной сигнал равен 0. Логическая функция называется: Запрет по Х2. Применяется на практике для блокировки прохождения управляющего сигнала Х1 в зависимости от значения сигнала Х2 (например, контроль наличия ограждения и других защитных барьеров).
__
Логическое уравнение функции: Y = Х1 Ù Х2 .
Поскольку переменные равноправны, переставив символы Х1 и Х2, получим функцию “Запрет по Х1” __
Y = Х2 Ù Х1.
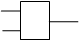
з) Цепь с реверсивными управляющими сигналами (ВПЕРЕД - НАЗАД).
Схема Таблица истинности
Х1 ¯ Х2 ¯
| Х1 | Х2 | Y |
Y
®
Х1 ¯ Х2 ¯
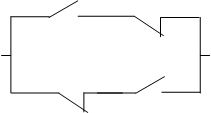
Рис.10.
Выходной сигнал Y будет равен 1, если Х1=1 ИЛИ Х2=1, но исключается случай, когда Х1 И Х2 равны 1. То есть цепь замкнута, если входные сигналы Х1 и Х2 разные. Эта логическая функция называется функцией неравнозначности, или функцией Исключающее ИЛИ(в англоязычной литературе - Exclusive OR или XOR), или функцией Сложения по модулю 2. Последнее название отражает то, что таблица истинности данной функции соответствует таблице арифметического сложения одноразрядного двоичного числа, когда при сложении 1 + 1 результат равен 0 и возникает перенос 1 в старший разряд. __ __
Логическое уравнение: Y = Х1 Ù Х2 Ú Х1 Ù Х2 = Х1 Å Х2,
где Å - символ сложения по модулю 2.
 Х1
Х1
Условное графическое обозначение функции: М2 Y
Х2
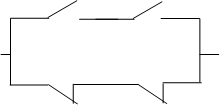
и) Цепь с последовательно включенными замыкающими и размыкающими контактами, соединенными параллельно.
Схема Таблица истинности
 Х1 ¯ Х2 ¯
Х1 ¯ Х2 ¯
| Х1 | Х2 | Y |
Y 
Х1 ¯ Х2 ¯
Рис.11.
Цепь будет замкнута, когда входные сигналы Х1, Х2 одинаковые. Это будет логическая функция равнозначности или эквивалентности.
___ ___ ________
Логическое уравнение цепи: Y = (Х1 Ù Х2) Ú ( Х1 Ù Х2 ) = Х1 Å Х2.
В заключение сделаем выводы о соответствии релейно-контактных схем и логических уравнений:
— замыкающий контакт соответствует переменной уравнения в прямой форме;
— размыкающий контакт схемы соответствует переменной уравнения в инверсной форме;
— последовательное соединение контактов соответствует конъюнкции (операции И) переменных;
— параллельное соединение контактов соответствует дизъюнкции (операции ИЛИ) переменных.
Получив начальные сведения по базовым логическим операциям и функциям, перейдем к изложению основных законов булевой алгебры.
Дата добавления: 2022-02-05; просмотров: 598;