МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Под задачей минимизации ЛФ понимается задача упрощения этих функций в целях уменьшения затрат на их аппаратурную реализацию. Минимальной будет считаться такая разновидность функции, которая состоит из наименьшего количества дизъюнктивных членов при наименьшем суммарном числе символов переменных. В основе методов минимизации ЛФ летит операция склеивания, а в качестве исходной формы ЛФ, как правило, выбирают СДНФ.

Введем некоторые определения.

Смежными или соседними называют минтермы, которые отличаются друг от друга формой вхождения только одной переменной.

Например, соседними являются минтермы Х1·Х2·Х3 и Х1·Х2·Х3, которые отличаются только формой вхождения Х3.

Минтермы Х1·Х2·Х3 и Х1·Х2·Х3 - не являются соседними.

Два соседних минтерма могут быть склеены. В результате получаем импликанту т.е. конъюкцию, число аргументов в которой на один меньше, чем в исходном минтерме.

При этом импликанта принимает значение 1 на тех же наборах переменных, что и исходная функция.

__ __ __ __ __ __

Х1·Х2·Х3 Ú Х1·Х2·Х3 = Х1·Х2·(Х3·Х3) = Х1·Х2; ( Х3·Х3 = 1),

__

импликанта Х1·Х2 не зависит от Х3.

Процесс склеивания может быть продолжен и для импликант, если они смежные:__ __ __ __ __ __ __ __

( Х1·Х2·Х3·Х4 Ú Х1·Х2·Х3·Х4) Ú ( Х1·Х2·Х3·Х4 Ú Х1·Х2·Х3·Х4 ) =

__ __ __

I - й этап: = Х1·Х2·Х4 Ú Х1·Х2·Х4 = (склеивание по Х3)

__

II - й этап: = Х1·Х2; (склеивание по Х4).

Итак, при склеивании двух соседних минтермов от n переменных получаем импликанту, которая зависит от (n-1) переменных, при склеивании четырех минтермов - от (n-2) переменных, восьми минтермов - от (n-3) переменных и, в общем случае, при склеивании (2 в степени m) соседних минтермов получаем импликанту от (n-m) переменных. Процесс многоступенчатого склеивания приводит к получению импликант, которые не склеиваются с другими. Такие импликанты называются простыми. Вместе с исходными минтермами, которые не имели соседних и не подвергались процессу склеивания, простые импликанты входят в результирующую ДНФ логической функции, которую называют сокращенной ДНФ.

Простые импликанты, наличие или отсутствие которых в сокращенной ДНФ

не сказывается на значении функции, называются избыточными.

Если из сокращенной ДНФ удалить все избыточные импликанты, то получим ДНФ, которую называют тупиковой. Логическая функция может иметь несколько тупиковых ДНФ. Искомая минимальная ДНФ совпадает (соответствует) с той тупиковой ДНФ, которая содержит минимальное число вхождений аргументов (букв).

Среди методов минимизации ЛФ наибольшее распространение получили метод Квайна и метод карт Карно.

Метод Квайна

Метод Квайна применяют к ЛФ, заданным в СДНФ. На первом этапе выполняется переход от СДНФ к сокращенной ДНФ путем проведения всех возможных склеиваний. Для этого каждый раз в группе конъюнкций отыскиваются пары A_i·x_i и A_i·x_i, где А_i - общая часть конъюнкций. С учетом закона повторения, каждая конъюнкция может участвовать в нескольких склеиваниях (т.е. она может иметь другую пару A_j·x_j и A_j·x_j ). Полученные импликанты вновь подвергают попарному сравниванию, и так до тех пор, пока не получим сокращенную ДНФ.

Пример:

__1__ __ __ 2 3__ __ 4__ 5

F = Х1·Х2·Х3 + Х1·Х2·Х3 + Х1·Х2·Х3 + Х1·Х2·Х3 + Х1·Х2·Х3.

Проверяем все возможные пары конъюнкций 1-2, 1-4, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5, 4-5 и находим, что склеивание возможно для пар 1-3, 2-5, 3-4, 4-5

( 4-я - 2 раза). __ __ __ __ __ __ __ __

F = ( Х1·Х2·Х3 + Х1·Х2·Х3 ) + ( Х1·Х2·Х3 + Х1·Х2·Х3 ) + (Х1·Х2·Х3 +

__ __ __1__ 2 3__ 4

Х1·Х2·Х3 ) + ( Х1·Х2·Х3 + Х1·Х2·Х3 ) = Х2·Х3 + Х2·Х3 + Х1·Х2 + Х1·Х3.

Опять сравниваем попарно конъюнкции 1-2, 1-3, 1-4, 2-3, 2-4, 3-4. Эти пары уже не смежные, не склеиваются, т.е. получили сокращенную ДНФ.

Второй этап метода Квайна заключается в переходе от сокращенной ДНФ к тупиковым ДНФ и выборе среди них минимальной ДНФ.

Для выявления лишних простых импликант строится импликантная матрица, которая иногда также называется таблицей покрытий. Каждая строка импликантной матрицы соответствует одной простой импликанте, а столбцы - конъюнкциям исходного выражения ( минтермам ).

1 2 3 4 5

	x1 x2 x3	x1x2x3	x1x2 x3	x1x2x3	x1x2x3
1) x2 x3	x		x
2) x2x3		x			х
3) x1x2			x	x
4) x1x3				х	х

Каждая импликанта сравнивается со всеми минтермами. Если импликанта является частью некоторого минтерма (то есть ее можно получить из минтерма зачеркиванием некоторых букв), то говорят, что импликанта поглощает (покрывает) минтерм, и на пересечении строки и столбца ставится условный знак-отметка. Покрытие означает, что на соответствующих наборах аргументов импликанта обеспечивает единичные значения логической функции. Для нашего примера импликанта (1) покрывает минтермы (1) и (3). Аналогично заполняем и другие строки таблицы. Минимальной ДНФ будет соответствовать такая система минимального количества строк таблицы, которая будет иметь отметки во всех столбцах, то есть будет обеспечивать покрытие всех минтермов. Рекомендуется следующий алгоритм выявления тупиковых ДНФ:

1) Выделяются все обязательные (или существенные) импликанты, которые имеют пометку, единственную в каком-либо столбце. Такие импликанты нельзя удалять, они обязательно будут присутствовать в минимальной ДНФ, и далее они не проверяются.

2) Среди оставшихся импликант условно вычеркиваем строку вместе с соответствующими пометками. Если после этого в каждом столбце таблицы останется хотя бы по одной отметке, то проверяемая импликанта является лишней, и ее можно удалить.

3) Испытание следующей импликанты проводим после удаления пометок выявленных лишних импликант. Изменение последовательности испытаний и удалений импликант может привести к различным тупиковым ДНФ, из которых выбираем минимальную.

Из таблицы примера видим, что простая импликанта (1) обеспечивает единичное значение логической функции на наборе 000 (и только эта импликанта, больше пометок в этом столбце нет), импликанта (2) - на наборе 011 (и она тоже единственная). Поэтому эти импликанты существенные, и их удалять нельзя. Простую импликанту (3) можно считать лишней и вычеркнуть. После этого импликанту (4) вычеркивать нельзя, она осталась единственной в четвертом столбце таблицы. Однако, если изменить порядок испытаний и сначала испытать импликанту (4), то ее можно удалить, но оставить импликанту (3).

В результате получаем две тупиковые ДНФ:

__ __ __

1) F1т = Х2·Х3+Х2·Х3+Х1·Х3, в которую не включена импликанта Х1·Х2;

__ __ __

2) F2т = X2·X3+X2·X3+X1·X2, в которую не включена импликанта Х1·Х3.

Тупиковые формы имеют одинаковое суммарное число переменных ( шесть ), поэтому любую из них можно выбрать в качестве минимальной ДНФ.

Для этого метода разработаны различные модификации, в том числе ориентированные на ЭВМ.

Метод карт Карно

Этот метод удобен для минимизации логических функций, содержащих не более 5-6 переменных.

Для минимизации ЛФ приводят к СДНФ и заполняют карту Карно.

Наличие единиц в соседних (по вертикали или по горизонтали) клетках карты соответствует смежным минтермам, которые могут быть склеены. Процесс группировки двух, четырех, восьми и т.д. клеток с единицами удобно проводить визуально, что оформляется в виде прямоугольного контура вокруг этих клеток, после чего можно записать ответ - тупиковую ДНФ в виде дизъюнкции (суммы) простых импликант, описывающих проведенные контуры. При наличии различных вариантов проведения контуров получаем несколько тупиковых ДНФ, среди которых выбираем минимальную.

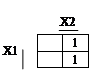Пример 1:

__ __

F (X1, X2) = X1·X2 + X1·X2= X1·( X2 + X2 ) = X1.

Видим, что в импликанте, описывающей контур, остаются те переменные, которые в пределах контура не меняют своего значения.

Правила проведения контуров:

1) внутри контура должны быть только клетки с единицами;

2) количество этих клеток с единицами должно выражаться величиной

2ⁱ ( i = 0, 1, 2, 3, ... ), то есть склеиванию может подвергаться одна клетка (нет склеивания ), две клетки ( минус одна переменная ), четыре клетки

1

( минус две переменных ), 8, 16 и т.д. ;

3) единицы в крайних клетках одного

столбца или строки могут включаться

в один контур, то есть карту можно

закручивать в трубку по обеим осям;

4) каждый контур должен включать как можно большее число клеток с единицами (2,4,8,..), а общее число контуров должно быть как можно меньшим;

5) каждая клетка может входить в несколько контуров, но каждый контур должен иметь как минимум одну единичную клетку, не входящую в другие контуры (нельзя проводить контур внутри другого контура).

В простую импликанту, описывающую каждый контур, включаются только те переменные, которые во всех клетках контура не меняют своего значения (то есть имеют прямое или инверсное вхождение).

Пример 2 (из метода Квайна). Имеется два варианта проведения контуров.

__ __ __ __ __ __ __

F(X1, X2, X3) = X1·X2·X3 + X1·X2·X3 + X1·X2·X3 + X1·X2·X3 + X1·X2·X3;

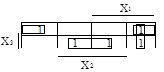
Рис.25. Первый вариант Рис.26. Второй вариант.

Fmin1 = Х2·Х3 + Х2·Х3 + Х1·Х3. Fmin2 = X1·X2 + X2·X3 + X2·X3.

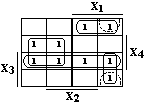
Пример 3: здесь такжевозможны два варианта проведения контуров через

правую нижнюю клетку.

__ __ __ __

а) F = X1·X3·X4+X1·X2·X3+X1·X4+X3·X4;

__ __ __ __ __

б) F = X1·X3·X4+X1·X2·X4+X1·X4+X3·X4.

Рис.27.

Видим, что при 4-х..5-ти переменных метод карт Карно проще метода Квайна, но визуальный метод проведения контуров, легко доступный человеку, плохо поддается алгоритмизации на ЭВМ.

При минимизации частично определенных ЛФ некоторым безразличным значениям функции присваивают значение 1, если это позволяет образовать более крупный контур, остальные считают равными 0. В результате получаем более простое выражение минимальной ЛФ.