Теорема разложения логических функций.
Любую логическую функцию F(X1,X2,...,Xp,...,Xn) можно разложить по переменной Xp :
__
F(X1,X2,..., XP,...,Xn)= XpÙF(X1,X2,...,0,...,Хn) Ú XpÙF(X1,X2,...,1,...,Xn) .
Докажем теорему методом перебора:
а) пусть переменная Xp=0, тогда
F(X1,X2,...,0,...,Xn)=1ÙF(X1,X2,...,0,...,Xn) Ú 0ÙF(X1,X2,...,1,...,Xn)=
=F(X1,X2,...,0,...,Xn),
т.е. теорема справедлива независимо от значений других переменных;
б) пусть переменная Xp=1, тогда
F(X1,X2,...,Xp,...,Xn)=0ÙF(X1,X2,...,0,...,Xn) Ú 1ÙF(X1,X2,...,1,...,Xn)=
=F(X1,X2,...,1,...,Xn),
и в этом случае теорема справедлива независимо от значений других переменных.
В результате получаем функцию, которая уже зависит от (n-1) переменной.
Продолжая разложение по другим переменным, в конце полного разложения получим дизъюнкцию всех переменных вида:
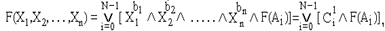
где: i=0,1, ..., (N-1); N=2n.;
C1i=Xb11ÙXb22Ù...ÙXbnn - минтерм;
F(Ai)-значение функции ( 0 или 1), которое она принимает на наборе Ai.
Например, разложение логической функции И будет иметь вид:
F(X1,X2)=C10×F(0)+C11×F(1)+C12×F(2)+C13×F(3)=C13×1 .
Форма записи, когда логическая функция представляется в виде дизъюнкции (логической суммы) минтермов, называетсясовершенной дизъюнктивной нормальной формой (СДНФ). Причем для представления логической функции достаточно рассматривать только те наборы переменных Ai, при которых F(Ai)=1 , т.к. C1iÙF(Ai)=0 при F(Ai)=0 .
Так для логической функции Исключающее ИЛИ:
__ __ F(X1,X2)=C10×0+C11×1+C12×1+C13×0=C11+C12=X1×X2+X1×X2 .
СДНФ легко получить из таблицы истинности логической функции, записав дизъюнкцию (логическую сумму) тех минтермов, при которых логическая функция принимает значение 1.
| i | X1 | X2 | X3 | F | |
Например, для произвольной логической
функция с заданной таблицей истинности:
__ __ __ __ __
F(X1,X2,X3)=X1×X2×X3+X1×X2×X3+X1×X2×X3+X1×X2×X3.
F(A0)=F(A3)=F(A4)=F(A6)=0 , их не учитываем.
Иногда СДНФ называют формой представ-
ления логической функции по единицам.
На основании закона двойственности теорему разложения и записи функции можно представить через конъюнкцию переменных:
__
F(X1,X2,...,Xp,...,Xn)=[ XpÚF(X1,X2,...,1,...,Xn) ] Ù [ XpÚF(X1,X2,...,0,...,Xn) ] ,
и в результате полного разложения по всем переменным получим конъюнкцию
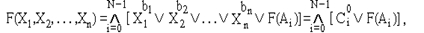
Здесь существенными являются только те наборы Ai, при которых F(Ai)=0, т.к. С0i Ú 1=1 независимо от значения C0i .
Это будет совершенная конъюнктивная нормальная форма (СКНФ), или форма представления по нулям.
Для рассмотренного выше примера представления функции в СДНФ эта же функция в СКНФ будет иметь вид:
__ __ __ __ __
F(X1,X2,X3)=(X1+X2+X3)×(X1+X2+X3)×(X1+X2+X3)×(X1+X2+X3).
Здесь рассматриваются только те строчки таблицы истинности, где функция равна нулю.
КАРТЫ КАРНО
При небольшом числе переменных удобным и наглядным является графическое представление логической функции в виде карт минтермов или в виде карт Карно.
Карта Карно состоит из q=2n клеток, причем каждой из клеток соответствует один из q минтермов. Карта представляется в виде квадрата или прямоугольника. Переменные разбиваются на две группы. Переменным одной группы ставят в соответствие столбцы, другой - строки. Переменные первой группы остаются постоянными в пределах каждого столбца, второй - постоянными в пределах строки. Каждой клетке ставится в соответствие определенный набор переменных.
Например, для двух переменных (n=2) имеем q= 22=4 клетки. На рисунках последовательно представлена карта Карно для двух переменных, клетам которой поставлены в соответствие алгебраическое выражение минтерма (рис.12), наборы значений переменных, при которых минтерм равен 1 (рис.13), и числовое (десятичное) представление набора переменных (рис.14).
 
| Х1 0 | Х1 0 | Х1 0 | |||||||
| Х2 | Х1Х2 | Х1Х2 | Х2 | Х2 | ||||||
| Х1Х2 | Х1Х2 |
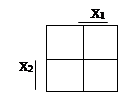 Рис. 12. Рис.13. Рис.14
Рис. 12. Рис.13. Рис.14
Значение переменной обычно задается в виде
черты по периметру карты:
черта есть – переменная в пределах строки или
столбца равна 1,
черты нет – переменная равна 0.
Рис.15.
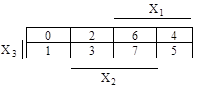
|
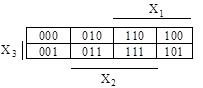
|
 Для трех переменных имеем карту Карно из 23=8 клеток, которым соответствуют следующие наборы переменных в двоичном и десятичном представлении. Здесь расположение переменных по битам принято Х1Х2Х3.
Для трех переменных имеем карту Карно из 23=8 клеток, которым соответствуют следующие наборы переменных в двоичном и десятичном представлении. Здесь расположение переменных по битам принято Х1Х2Х3.
Рис.16. Рис.17.
| __ __ __ __ X1 X2 X3 X4 | __ __ __ X1 X2 X3 X4 | __ __ X1 X2 X3 X4 | __ __ __ X1 X2 X3 X4 |
| __ __ __ X1 X2 X3 X4 | __ __ X1 X2 X3 X4 | __ X1 X2 X3 X4 | __ __ X1 X2 X3 X4 |
| __ __ X1 X2 X3 X4 | __ X1 X2 X3 X4 | X1 X2 X3 X4 | __ X1 X2 X3 X4 |
| __ __ __ X1 X2 X3 X4 | __ __ X1 X2 X3 X4 | __ X1 X2 X3 X4 | __ __ X1 X2 X3 X4 |
|
|
|
Для четырех переменных имеем карту Карно из 24=16 клеток.
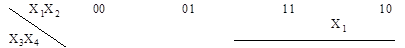
|


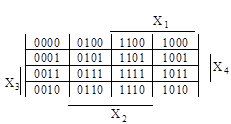
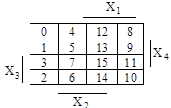
Рис.19. Рис.20.
Здесь каждой клетке карты поставлены в соответствие выражение минтерма (рис.18), двоичное (рис.19) и десятичное (рис.20) представления набора переменных при расположении переменных по битам Х1Х2Х3Х4. При изменении порядка расположения битов изменится десятичное представление.
Аналогично, при n=5 имеем 32 клетки, при n=6 - 64 клетки.
Приведенное распределение переменных по строкам и столбцам не является единственным. Обязательным требованием является только то, что переменные по сторонам распределяются так, чтобы при переходе из клетки в клетку по вертикали или горизонтали происходила инверсия только одной переменной.
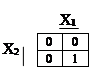
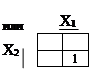 Для представления логической функции в виде карты Карно в соответствующую клетку карты вписывается 1, если логическая функция равна 1 на данном наборе переменных, и вписывается 0 или клетка оставляется пустой, если логическая функция равна 0.
Для представления логической функции в виде карты Карно в соответствующую клетку карты вписывается 1, если логическая функция равна 1 на данном наборе переменных, и вписывается 0 или клетка оставляется пустой, если логическая функция равна 0.
Логическая функция “И”:
Y = X1 Ù X2.
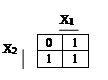 Рис.21.
Рис.21.

Логическая функция “ИЛИ”:
Y = X1 Ú X2 =
= X1 Ù X2 Ú X1 Ù X2 Ú X1 Ù X2.
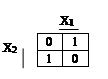 Рис.22.
Рис.22.
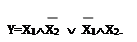 Логическая функция “Исключающее ИЛИ”:
Логическая функция “Исключающее ИЛИ”:
Рис.23.
Для произвольной логической функции карта Карно представляет собой совокупность клеток, заполненных “1”, каждой из которых соответствует минтерм в СДНФ логических функций.
Например: Х1
 __ __ __ __
__ __ __ __
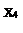
 F (X1,X2 ,X3,X4) = X1 X2 X3 X4+
F (X1,X2 ,X3,X4) = X1 X2 X3 X4+
 __ __ __ __ __X3
__ __ __ __ __X3
+X1X2X3X4 + X1X2X3X4 + X1X2X3X4 .
 |
Рис. 24. Функция и ее карта Карно.Х2
Клетки, содержащие 1, называются “1-клетками”, а клетки, содержащие 0, - “0-клетками”. Логические функции, имеющие определенные значения (0 или 1) при всех возможных наборах переменных, называются полностью определенными. Имеются функции, значения которых определены только для части наборов переменных. Такие логические функции называются частично определенными. Те наборы значений аргументов, для которых значение функции не определено, будем называть безразличными, на карте Карно эти клетки будем указывать знаком “х”. Этим наборам соответствуют ситуации, которые на практике никогда не реализуются. Частично определенную функцию можно доопределить, приписав безразличным значениям произвольно 0 или 1. Обычно доопределение проводят таким образом, чтобы, используя законы алгебры логики, упростить выражение.
Дата добавления: 2022-02-05; просмотров: 751;











