Аксиомы проективного пространства
Рассмотрим (п+1)-мерное векторное пространство - Vn+1 , исключим из него нулевой вектор ō - Vn+1 / {ō} = V 0n+1.
Замечание: Vn+1 - можно брать над любым полем. Мы в дальнейшем будем брать векторное пространство над полем действительных чисел. В общем случае поле может быть как бесконечным, так и конечным.
Определение: Множество Pn ≠Ø называется п- мерным проективным пространством, если существует некоторое отображение φ: V 0n+1 → Pn ,удовлетворяющее условиям:
1. φ-сюръекция (любой элемент из Pn имеет хотя бы один прообраз).
2. 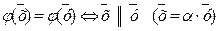 (образы равны тогда и только тогда, когда прообразы коллинеарны).
(образы равны тогда и только тогда, когда прообразы коллинеарны).
Эти условия называются аксиомами проективного пространства. В этом случае говорят, что Vn+1 - векторное пространство порождает Pn -проективное пространство.
Если Vn+1 содержит Lm+1 - подпространство, то оно в свою очередь будет порождать Pm проективное подпространство в Pn.
Частные случаи:
· проективное пространство P3 порождено V4;
· проективная P2 порождена V3 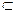 V4
V4  P2
P2 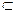 P3 ;
P3 ;
· проективная прямая P1 порождена
V2 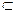 V3
V3 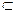 V4
V4  P1
P1 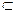 P2
P2 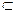 P3 ;
P3 ;
· проективная точка P0 порождена
V1 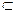 V2
V2  V3
V3  P0
P0  P1
P1  P2.
P2.
Дата добавления: 2022-02-05; просмотров: 625;











