Преобразование ЛФ к базису ИЛИ-НЕ

За основу следует взять СКНФ ЛФ и использовать закон двойного отрицания.

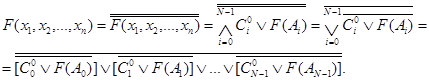
Сначала выполняют операцию ИЛИ-НЕ на макстермах [CiÚF(Ai)], а затем операция ИЛИ-НЕ над результатом.

Как и СДНФ, СКНФ сначала следует минимизировать. Практическая последовательность получения минимальной КНФ может быть следующей: __

а) сначала находим инверсную МДНФ F с помощью карт Карно, но контуры проводим вокруг 0-клеток. Правила записи суммы минтермов те же. Для дополнительной минимизации можно в контуры включать безразличные (неопределенные) значения логической функции;

б) инвертируя выражение функции 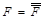и применяя правило де Моргана, получаем минимальную КНФ.

Рис.31. Пример логической функции (для сравнения функция та же, что и для преобразования в базис И-НЕ).

_ __ __ __ __

а) F = X1×X3 + X2×X3 + X2×X3×X4;

б) приводим к конъюктивной нормальной форме:

(рис.32)

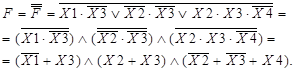
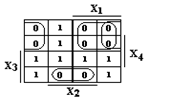
Минимальную КНФ можно получить сразу из карты Карно. Проводим контуры вокруг 0-клеток. Каждому контуру соответствует макстерм (сумма, дизъюнкция) переменных, не изменяющих форму вхождения внутри контура. Если переменная на контуре имеет значение 0, то в макстерм она записывается в прямой форме, если равна 1, то в инверсной форме.

Подвергая МКНФ двойной инверсии и используя правило де Моргана, приводим ЛФ к базису ИЛИ-НЕ. Для рассмотренного примера МКНФ в базисе ИЛИ-НЕ:

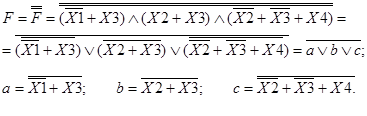
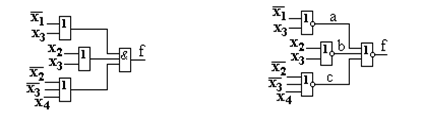
Рис.32. Схема в базисе И, ИЛИ, НЕ. Рис.33. Схема в базисе ИЛИ-НЕ.

В результате мы получили четыре варианта реализации логической функции: а) конъюктивная форма в базисе И, ИЛИ, НЕ (рис.29); б) дизъюнктивная форма в базисе И, ИЛИ, НЕ (рис.32); в) в базисе И-НЕ (рис.30); г) в базисе ИЛИ-НЕ (рис.33).