III. Аксиомы дистрибутивности

(А 6 )" a, b, c Î K a× (b + c) = a× b + a× c (дистрибутивность

(А 7)" a, b, c Î K (a + b) × c = a× c + b× c сложения и умножения)

Примеры: 1.(Z, +,× ), (Q, +, × ), (R, +, × ), (C, +, × ) – числовые кольца.

2.(M_nn( F), +, × ) – кольцо квадратных матриц порядка n.

3. (F[x], +, ×) – кольцо многочленов от одного переменного x над полем F.

4. (Z_n , +, × ) – кольцо классов вычетов по модулю n.

5.(N, +, × ) – не кольцо.

Определение 1.4. Кольцо (K, +, ∙) называется коммутативным, если выполняется аксиома коммутативности умножения.

(А8):" a, b Î G a · b = b · a

Определение 1.5.Кольцо (K, +, ∙) называется кольцом с единицей, если выполняется аксиома существования единицы по умножению:

(А 9):$ 1Î G " a Î G a · 1 = a = 1 · a (существование единицы)

Примеры: 1. Все перечисленные кольца являются кольцами с единицами (в кольце матриц единицей будет единичная матрица Е_n).

2. Кольцо матриц (M_nn(F), +, ×)при n ³ 2некоммутативно, остальные перечисленные кольца коммутативны.

3. Кольцо (2×Z, +, ×)чётных целых чисел является коммутативным кольцом без единицы.

4.Кольцо матриц вида({ 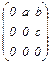| a, b, c Î F},+, ×)является некоммутативным кольцом без единицы.

Определение 1.6. Коммутативное кольцо (F, +, × )с единицей 1называется полем, если выполняются следующие аксиомы:

(А10):" a Î F (а 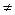0)$ a^–1 Î F a× a^–1 = 1 = a^–1× a (обратимость всех ненулевых элементов)

(А11):1 ¹ 0(нейтральные элементы относительно сложения и умножения различны)

Примеры: 1. Среди перечисленных колец полями будут числовые поля (Q,+,×), (R, +, ×),(C, +, ×)и поле классов вычетов (Z_n ,+, × )по модулю простого числа n = p.

2. Кольцо (Z, +, ×)полем не является, т.к. не выполнено (А10).