Точкова оцінка дисперсії. Виправлена дисперсія

За точкову оцінку дисперсії беруть вибіркову дисперсію 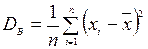, яка є зміщеною оцінкою параметра 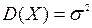. Цей факт випливає з рівності 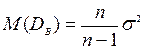, яку неважко встановити за допомогою безпосередніх обчислень. Тому вибіркову дисперсію доцільно виправити таким чином, щоб вона стала незміщеною оцінкою. Для цього достатньо 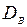помножити на дріб .

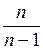Виправлену вибіркову дисперсію позначають .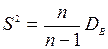

Тоді виправленим середньоквадратичним відхиленням вибірки буде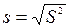

Дріб 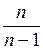називають поправкою Бесселя. Для малих п поправка Бесселя значно відрізняється від одиниці. Для п>50 практично немає різниці між 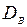і .

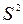Можна показати, що оцінки 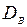і 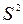є змістовними і не є ефективними.

У випадку, коли математичне сподівання а відоме і випадкова величина Х нормально розподілена, то незміщеною, змістовною та ефективною оцінкою дисперсії 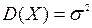є оцінка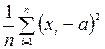

Точкові оцінки параметрів розподілу є випадковими величинами, їх можна вважати первинними результатами обробки вибірки тому, що невідомо, з якою точністю кожна з них оцінює відповідну числову характеристику генеральної сукупності.

Однак, при малому об’ємі вибірки точкові оцінки можуть мати значні розходження із значенням параметра, що оцінюється. Це призводить до грубих помилок.

Більш точними є інтервальні оцінки.

Означення. Інтервальноюназивають оцінку, яка визначається двома числами – кінцями інтервалу.

Інтервальні оцінки дозволяють встановити точність та надійність оцінок.

Нехай за даними вибірки знайдена статистична оцінка 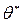невідомого параметра 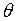, який бдемо вважати сталим числом. Очевидно, що 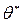тим точніше визначає параметр 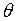, чим менша за абсолютною величиною різниця .

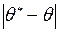Означення. Число δ, для якого виконується нерівність 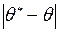<δ, називають точністю оцінки.

Означення. Надійністю оцінки 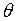по 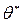називають ймовірність γ, з якою виконується нерівність 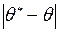< δ або

γ=Р( 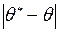<δ) (20)

Найчастіше число γ задається наперед і, залежно від обставин дорівнює 0,95 або 0,99, або 0,999.

Замінимо нерівність 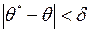на рівносильну .

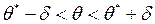Звідси формулу (20) можна переписати у такому вигляді

.

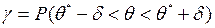Означення. Інтервалом довір’я або довірчим інтервалом називають інтервал 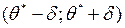, який із заданою надійністю 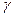покриває невідомий параметр .

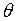Зауваження. Кінці довірчого інтервалу є випадковими величинами.