Інтервальні оцінки для математичного сподівання

Теорема 1.Нехай Х – нормально розподілена ознака генеральної сукупності, для якої М(Х)=а, 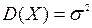, 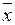– вибіркова середня, обчислена за вибіркою обсягом п з цієї генеральної сукупності. Тоді

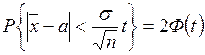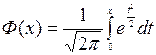" t > 0 , де . (21)

Теорема 2.Нехай Х – довільно розподілена ознака генеральної сукупності, для якої М(Х)=а, 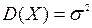, 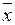– вибіркова середня, обчислена за вибіркою обсягом п з цієї генеральної сукупності. Тоді

" t > 0 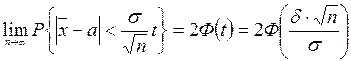, (22)

де .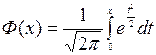

Нехай х₁, х₂, х₃, ..., х_n – результати п незалежних спостережень за випадковою величиною Х, на підставі яких необхідно знайти інтервал довір’я для невідомого параметра а=М(Х) .

Оскільки для математичного сподівання точковою оцінкою є 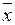, то для знаходження інтервалу довір’я 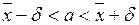потрібно розв’язати рівняння

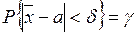Û 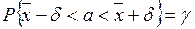, (23)

якщо середнє квадратичне відхилення 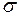випадкової величини Х відоме, то розв’язок рівняння (23) можна знайти використовуючи рівності (21) або (22).

Так, якщо 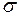відоме, Х- нормально розподілена випадкова величина або обсяг вибірки значний (п >30), то ми можемо записати, що

.

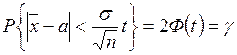Тоді, якщо 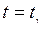– розв’язок рівняння 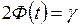, то з надійністю 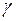інтервал 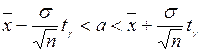є інтервалом довір’я для математичного сподівання а.

Якщо 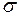невідоме, але обсяг вибірки значний (п >30), то інтервал довір’я можна записати у вигляді

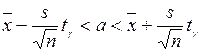або 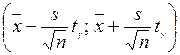, (24)

де s – виправлене середньоквадратичне відхилення, знайдене за вибіркою обсягу п.

Якщо 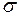невідоме, обсяг вибірки незначний (п < 30), але Х- нормально розподілена випадкова величина то інтервал довір’я можна записати у вигляді (24), де значення 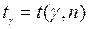шукають за таблицями значень для розподілу Стьюдента залежно від ймовірності 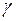і числа ступенів свободи k=n-1 (додаток 5).

Приклад. Вибіркове обстеження прибутків за місяць підприємців дало результати, дані якого записані у вигляді розподілу

Прибуток тис.грн.(хі)
Частота (kі)

Побудувати інтервал довір’я для математичного сподівання а, допустивши, що генеральна сукупність Х розподілена нормально з надійністю 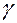=0.95.

Розв’язання.

Обчислимо числові характеристики вибірки

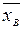=(1+3+8+15+12+7)/10=4,8

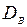=(1+9+16·2+25·3+36·2+49)/10-48 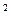=23,8-23,04=0,76

Виправлене середнє квадратне відхилення

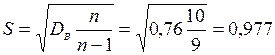
При надійності 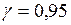та кількості ступенів вільності k=10-1=9 за таблицями додатку 5 знаходимо 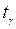=2.31. Підставивши обчислені та знайдені за таблицею значення у формулу (24), отримаємо інтервал довір’я (4,09;5,51) для щомісячних прибутків підприємств у тис.грн. з надійністю 0,95.