Тема 2. Аппроксимация

Аппроксимация – замена одной функции f(x) другой, похожей функцией Q(x). Например, функцию, полученную экспериментально в виде таблицы или графика, надо записать в аналитическом виде, либо функцию, достаточно сложную нужно заменить похожей, но более простой.

Простейший способ аппроксимации – замена функции f(x) алгебраическим полиномом

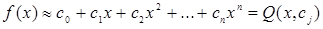(2.1)

Аппроксимацию называют точечной, если f(x) задана на конечном множестве точек (узлов)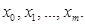

Если f(x) задана на непрерывном множестве значений аргументов, то аппроксимацию называют интегральной.

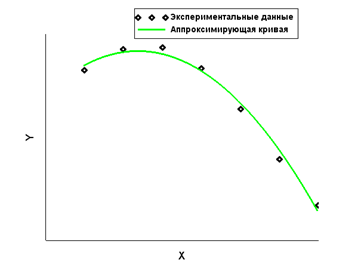
Рис. 2.1. Точечная аппроксимация

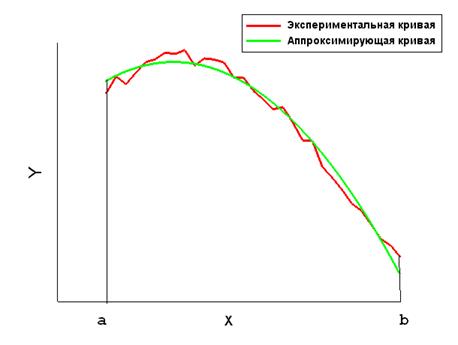
Рис. 2.2. Интегральная аппроксимация

Необходимо так подобрать коэффициенты аппроксимирующей кривой, чтобы Q(x) как можно меньше отличалась от f(x).

Мерой погрешности аппроксимации назовем некоторое неотрицательное число m(f, Q). Естественно потребовать, чтобы m(f,Q)=0, если f(x) и Q(x,c_j) совпадают на общем для их задания множестве значений аргументов. Справедливо и обратное утверждение.

После того, как мера каким-либо образом задана, необходимо указать способ получения коэффициентов с_j. Наиболее часто используемыми подходами к решению задачи аппроксимации являются метод наименьших квадратов (МНК), метод наименьших модулей и минимаксный подход.