Уточнение корня методом деления отрезка пополам
Уточнить корень – значит найти его приближенное значение с заданной погрешностью e.
Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.
Предположим, что отрезок [a, b], на котором отделен корень уравнения, уже найден.
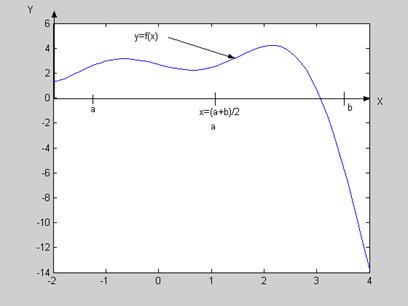
Пусть, например, f(a)>0, f(b)<0. Вычислим точку 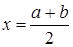 . Если вместо корня взять точку x, то погрешность, которую мы при этом допустим, не превысит величины
. Если вместо корня взять точку x, то погрешность, которую мы при этом допустим, не превысит величины 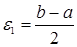 . Если эта погрешность не превышает некоторую заданную погрешность e, с которой нужно уточнить корень уравнения, то вычисления прекращаем и можно записать:
. Если эта погрешность не превышает некоторую заданную погрешность e, с которой нужно уточнить корень уравнения, то вычисления прекращаем и можно записать: 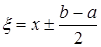 . В противном случае определяем новый отрезок [a, b], на котором отделен корень нашего уравнения. Для этого нам нужно знать знак функции в точке х. В нашем примере f(x)>0. Новый отрезок – отрезок [x, b], так как на концах этого отрезка функция имеет разные знаки. Переобозначим один из концов отрезка – в нашем случае положим a=x – и повторим процедуру для нового отрезка [a, b].
. В противном случае определяем новый отрезок [a, b], на котором отделен корень нашего уравнения. Для этого нам нужно знать знак функции в точке х. В нашем примере f(x)>0. Новый отрезок – отрезок [x, b], так как на концах этого отрезка функция имеет разные знаки. Переобозначим один из концов отрезка – в нашем случае положим a=x – и повторим процедуру для нового отрезка [a, b].
Метод касательных
Дополнительные предположения: f(x) дважды непрерывно дифференцируема на отрезке [a, b], на котором отделен корень; 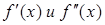 сохраняют постоянные знаки на отрезке [a, b]. Это – условия сходимости метода касательных. То есть выполнение этих условий гарантирует нам, что за определенное число шагов (вычислений по формуле (1.6)) мы уточним корень с любой заданной погрешностью ε. Вот алгоритм метода касательных.
сохраняют постоянные знаки на отрезке [a, b]. Это – условия сходимости метода касательных. То есть выполнение этих условий гарантирует нам, что за определенное число шагов (вычислений по формуле (1.6)) мы уточним корень с любой заданной погрешностью ε. Вот алгоритм метода касательных.
За х0 выбирается точка, в которой выполняется условие:
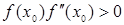 (1.5)
(1.5)
Это либо точка a, либо точка b. Далее вычисляются точки
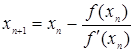 (1.6)
(1.6)
до тех пор, пока не выполнится условие
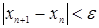 (1.7)
(1.7)
Тогда 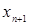 - приближенное значение корня с погрешностью e.
- приближенное значение корня с погрешностью e.
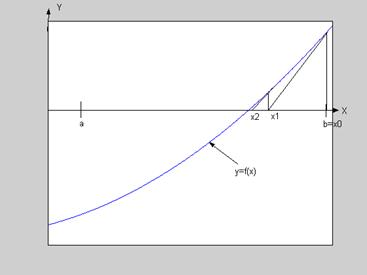
Проверим условия сходимости для нашего уравнения.
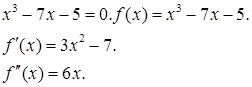
Предположим, мы хотим уточнить корень уравнения, отделенный на отрезке [2, 3]. Минимальное значение первой производной достигается в точке х=2 и оно положительно. Вторая производная положительна при любом х>0. В видеолекции https://youtu.be/U2787R9nlUY рассмотрен другой способ проверки условий сходимости. Там же показано, как можно выполнить 1 задание (в нашем курсе задания на эту тему – задания 3 и 4).
Далее. Выбираем точку х0. Это либо точка a (2 в нашем случае), либо точка b (3). Выясним, какая именно. Проверим, в какой из точек выполняется условие:
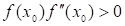
В точке a=2 f(a)<0, в точке b=3 f(b)>0: 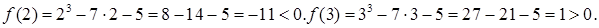
Поэтому х0=3. 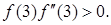
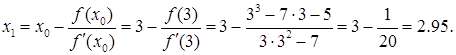
Предположим, что погрешность, с которой мы хотим уточнить корень, равна ε=0.1.
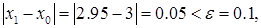 поэтому х1 можно считать корнем уравнения с заданной погрешностью:
поэтому х1 можно считать корнем уравнения с заданной погрешностью: 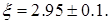 Если бы это оказалось не так, то нужно было найти х2, вычислить разность |x2-x1| и если она меньше ε, то х2 – корень уравнения с заданной погрешностью и т.д.
Если бы это оказалось не так, то нужно было найти х2, вычислить разность |x2-x1| и если она меньше ε, то х2 – корень уравнения с заданной погрешностью и т.д.
Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f), где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.
Покажем, как можно найти все три корня нашего уравнения.
clc
function y=f(x), y=x^3-7*x-5; endfunction
[a,b]=fsolve([-2,-1,3],f);disp([a;b])
-2.1660127 -0.7828157 2.9488284
-1.776D-14 1.510D-14 3.553D-14
Здесь в качестве начальных приближений выбраны точки -2, -1 и 3.
Если нам нужен только один корень уравнения, например, ближайший к точке 3, то изменяем оператор fsolve: [a,b]=fsolve(3,f). Запустив измененную программу на выполнение, получим:
2.9488284
3.553D-15
Первое число – это корень уравнения, второе – значение левой части уравнения в этой точке (3.553·10-15).
Решить алгебраическое уравнение в Scilab можно и с помощью функции roots.
В нашем примере: х3-7х-5=0. Задаем вектор коэффициентов полинома, идущих в порядке уменьшения степеней: сначала коэффициент перед х3, потом перед х2 и т.д. Затем используем функцию roots:
--> a=[1 0 -7 -5];x=roots(a)
x =
2.9488284
-2.1660127
-0.7828157
Систему нелинейных уравнений также можно решить, используя функцию fsolve.
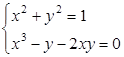
clc
function [y]=ff(x)
y(1)=x(1)^2+x(2)^2-1;
y(2)=x(1)^3-x(2)-2*x(1)*x(2);
endfunction
[t,value]=fsolve([-.5;-.5],ff);
disp([t,value])
-0.4492543 0.
-0.8934039 -8.771D-15
Однако, как и при решении уравнения, точность решения часто зависит от того, насколько удачно мы задали начальное приближение x0. В разделе 1.4 показано, как можно задать начальное приближение при решении систем двух нелинейных уравнений.
Вот пример решения уравнения рассмотренными методами.
Пример.Решить уравнениеex-x-7=0
Решение.
1 этап. Отделяем корень. Для этого строим график функции y=ex-x-7
clc
clf()
function y=f(x)
y=exp(x)-x-7
endfunction
x=1:.01:3;
plot(x,f(x));xgrid()
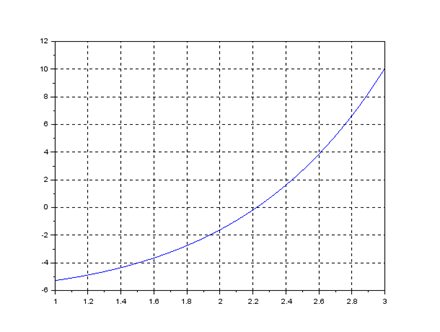
Из графика видно, что корень отделен на отрезке [2, 3].
2 этап. Уточнение корня с погрешностью ε=0.05.
Метод деления отрезка пополам
Обозначим f(x)=ех-х-7.
f(2)=e2-2-7= -1.6109439; f(3)= e3-3-7= 10.085537
x=(2+3)/2=2.5 Если взять точку х в качестве корня, то погрешность не превысит (3-2)/2=0.5.
f(2.5)=e2.5-2.5-7= 2.682494. Корень находится на отрезке [2, 2.5] так как на концах отрезка функция имеет разные знаки.
x=(2+2.5)/2=2.25 ξ=2.25±0.25 f(2.25)=e2.25-2.25-7= 0.2377358 Корень находится на отрезке [2, 2.25] так как на концах отрезка функция имеет разные знаки. x=(2+2.25)/2=2.125 ξ=2.125±0.125 и т.д., пока погрешность не станет меньше или равна заданной.
Метод касательных
Проверим условия сходимости.
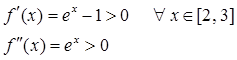
x0=3 т.к. 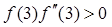 x1= x0-f(x0)/f’(x0)=3-(e3-3-7)/(e3-1)= 2.47.
x1= x0-f(x0)/f’(x0)=3-(e3-3-7)/(e3-1)= 2.47.
|x1-x0|=0.53>eps=0.1 x2= x1-f(x1)/f’(x1)=2.47-(e2.47-2.47-7)/(e2.47-1)=2.25
|x2-x1|=0.22>eps=0.05 x3= x2-f(x2)/f’(x2)=2.25-(e2.25-2.25-7)/(e2.25-1)=2.22
|x3-x2|=0.03<eps=0.05
Ответ: корень уравнения ξ=2.22±0.05
Дата добавления: 2022-02-05; просмотров: 460;











