Метод наименьших квадратов
2.1.1.1. Аппроксимация полиномами
Чаще всего при точечной аппроксимации используют меру
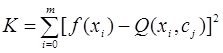 (2.2)
(2.2)
а коэффициенты сj ищут из условия
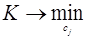 (2.3)
(2.3)
Это точечная квадратичная аппроксимация.
При интегральной аппроксимации
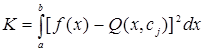

Описанный подход к задаче аппроксимации называется методом наименьших квадратов. Условия (2.2) и (2.3) геометрически означают: из всех кривых заданного вида выбирают ту, у которой сумма площадей квадратов отклонений – наименьшая. В математике кривую y=Q(x,cj) называют регрессией Y на X. Это означает, что у функции y=Q(x,cj) число искомых коэффициентов меньше количества узлов, в крайнем случае возможно равенство n+1£m+1. Здесь n степень аппроксимирующего полинома, а m – номер последнего узла (нумерация ведется с нуля).
Если аргументом считать y, а x – функцией, то говорят о регрессии X на Y. Отклонения в этом случае откладывают по оси X.

Рис. 2.3. Регрессия Y на X
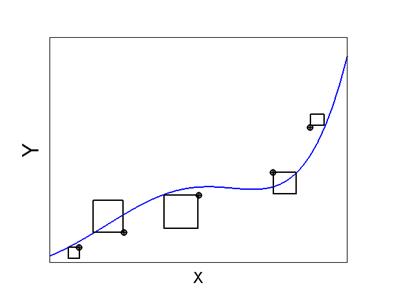
Рис. 2.4. Регрессия X на Y
Покажем, как находятся коэффициенты cj при точечной аппроксимации методом наименьших квадратов.
Минимальное значение K в формуле (2.2) достигается при тех сj, при которых
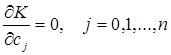 (2.4)
(2.4)
Имеем:
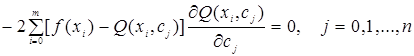 (2.5)
(2.5)
Здесь 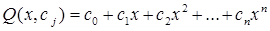 .
.
Обозначим 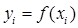 . Тогда система уравнений (2.4) примет вид (2.6):
. Тогда система уравнений (2.4) примет вид (2.6):
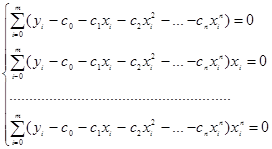 (2.6)
(2.6)
Окончательно
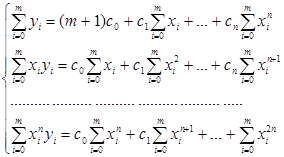 (2.7)
(2.7)
Здесь xi и yi – заданные числа.
Пример 2.1: Методом наименьших квадратов построить аппроксимирующую параболу для функции
| x | ||||
| y | -1,2 | -0,1 | 1,3 | 1,8 |
Составим таблицу
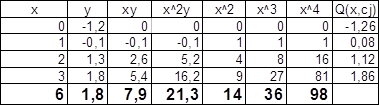
Запишем систему нормальных уравнений для нашей кривой.
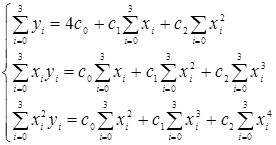 или
или 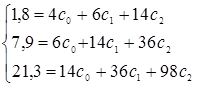
Решая систему, получаем:
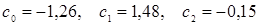 или
или 
Вычисляя K по формуле (2.2), получаем: K=0,0720. У любой параболы второй степени значение K, вычисленное по формуле (2.2), будет больше, чем 0,0720.
Решение задачи аппроксимации в Excel
Одним из самых простых и быстрых способов решения задачи аппроксимации является решение задачи в Excel.
Excel предлагает такие виды аппроксимирующей кривой (MS Office 2016): экспоненциальная (y=aebx), линейная (y=a+bx – установлена по умолчанию), логарифмическая (y=a+blnx), полиномиальная (степень полинома задает пользователь), степенная (y=axb). Предусмотрена также линейная фильтрация.
Покажем, как можно решить пример 2.1 в Excel. Вводим исходные данные. Выделяем столбцы x и y. На вкладке «Вставка» в раскрывающемся меню «Диаграммы» выбираем вид диаграммы «Точечная».
Получаем график, на который нанесены исходные данные (рис. 2.5).
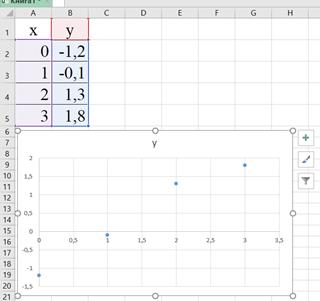
Рис. 2.5. Исходные данные на графике в Excel
Щелкнув правой кнопкой мыши по одной из синих точек, в раскрывающемся подменю выбираем пункт «Добавить линию тренда». В появившемся диалоговом окне «Формат линии тренда» (рис. 2.6) выбираем нужный тип кривой.
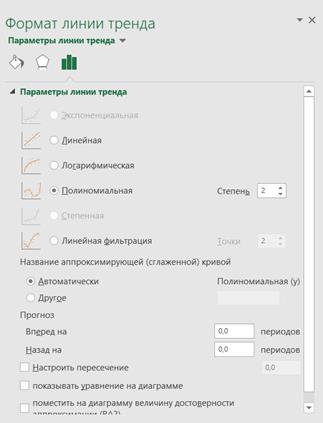
Рис. 2.6. Формат линии тренда
В нашем случае это полиномиальная кривая. Поставив точку слева от нужной надписи, выбираем степень аппроксимирующего полинома. По умолчанию стоит степень 2, которую будем использовать для расчетов. Поставив галочки слева от надписей «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации» (о коэффициенте R2 см. ниже), после редактирования диаграммы получим линию тренда (рис.2.7).

Рис. 2.7. Исходные данные и линия тренда
Убеждаемся, что получившееся уравнение совпадает с приведенным на с. 14.
Уравнения других типов кривых получаются аналогично.
При решении задачи аппроксимации в Excel выдается коэффициент достоверности аппроксимации (детерминации)
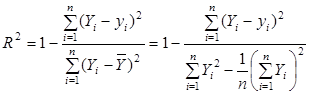
Здесь Yi – исходные данные, yi – значение аппроксимирующей кривой в точках таблицы.
Решение задачи аппроксимации в среде Scilab
Для поиска коэффициентов сi в формуле (2.1) в Scilab используется функция datafit:
[a, S]=datafit(F,z,c)
Здесь F –специальным образом заданная функция.
Для решения задачи задается вектор начальных приближений с. Размерность вектора равна количеству искомых коэффициентов. z – матрица исходных данных размерности 2 х n, состоящая из n пар значений (xi, yi).
Значение функции F в точке xi равно невязке:
 .
.
Результатом работы функции datafit являются искомые коэффициенты (они обозначены как вектор а) и S – сумма площадей квадратов отклонений (см. формулу 2.2). Начиная с версии Scilab 6.1.0 смысловая нагрузка выходного параметра S изменилась. В приведенных ниже программах значения суммы квадратов отклонений вычислялись непосредственно по формуле 2.2.
Вот решение примера 2.1 с использованием функции datafit:
Программа на Scilab:
clf();clc
//Функция, вычисляющая разность между экспериментальными
//и теоретическими значениями,
//перед использованием необходимо определить
//z=[x;y] - матрицу исходных данных и
//с - вектор начальных значений коэффициентов,
//размерность вектора должна совпадать
//с количеством искомых коэффициентов
function y=G(c,z)
y=z(2)-c(1)-c(2)*z(1)-c(3)*z(1)^2
endfunction
//Исходные данные
x=[0 1 2 3];y=[-1.2 -0.1 1.3 1.8];
//Формирование матрицы исходных данных
z=[x;y];//та же буква, что и в функции y=G(c,z)
//Вектор начальных приближений
c=[0;0;0];//нулей столько, сколько искомых коэффициентов. Это нач. приближение
a=datafit(G,z,c); //Решение задачи
//Нанесение на график экспериментальных данных
plot2d(x,y,-4);
//Построение графика функции на отрезке [xmin , xmax]
t=min(x):0.01:max(x);Ptc=a(1)+a(2)*t+a(3)*t^2;plot2d(t,Ptc);
err=sum((y-a(1)-a(2)*x-a(3)*x.^2)^2)//Сумма квадратов отклонений
disp("err=", err)
disp("a=", a)
Запустив программу на выполнение, получаем:
"err="
0.0720000
"a="
-1.2600001
1.4900003
-0.1500001
Ниже приведен график получившейся кривой.
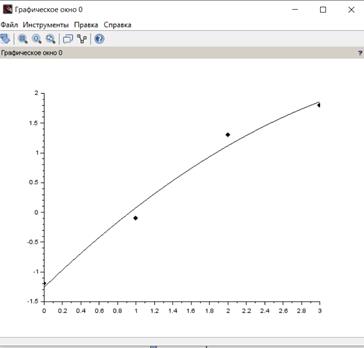
Дата добавления: 2022-02-05; просмотров: 467;











