Графический метод отделения корня

Отделение корня

Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

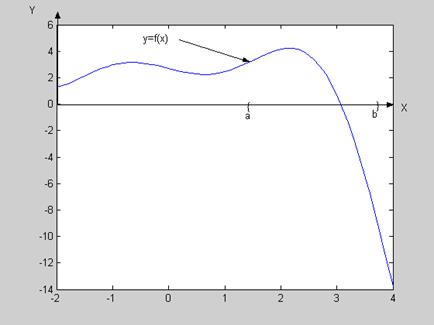
Отделить корень – значит указать такой отрезок [a, b] , на котором содержится ровно один корень уравнения .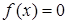

Не существует алгоритмов отделения корня, пригодных для любых функций f(x). Если удастся подобрать такие a и b, что

1) f(a) f(b)<0 (1.2)

2) f(x) – непрерывная на [a, b] функция (1.3)

3) f(x) – монотонная на [a, b] функция(1.4)

то можно утверждать, что на отрезке [a, b] корень отделен.

Условия (1.2) – (1.4) – достаточные условия того, что корень на [a, b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.

Корень можно отделить аналитически и графически.

Пример. Аналитически отделить положительный корень уравнения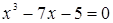

Решение. Составим таблицу

x
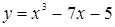
	-5	-11	-11

1) f(2)f(3)<0,

2) f(x) – непрерывная функция,

3) 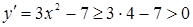, следовательно, f(x) – монотонно возрастает на отрезке [2, 3].

Вывод: на отрезке [2, 3] корень отделен.

Графический метод отделения корня

С учетом того, что существует много программных продуктов для построения графиков функций, можно построить график в одном из них. Покажем, как это можно сделать в Scilab.

Пример:

Составим программу:

clc

clf()

x=-4:.1:-3;y=x^3-7*x-5;

plot(x,y)

xgrid()

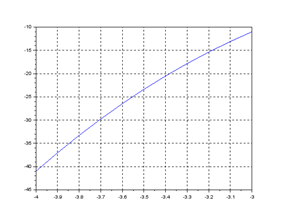
Из графика видно, что корня уравнения на отрезке [-4, -3] нет. Изменим пределы изменения аргумента, например, на следующие: [-4, 4]. Шаг можно оставить прежним. Получим:

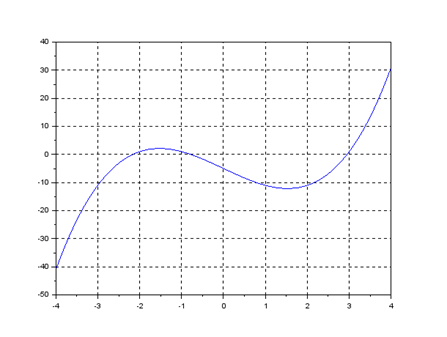
Из графика видно, что уравнение х³-7х-5=0 имеет три корня и в качестве отрезков, на которых отделен корень уравнения, можно выбрать, например, такие: [-2.5, -1.5], [-1.5, 0.5], [2, 3].