Распределение Стьюдента
Распределение Стьюдента (t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student) характеризует распределение случайной величины
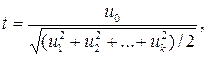
где u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента
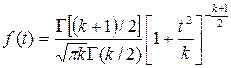 (3.5)
(3.5)
Величина k характеризует количество степеней свободы. Плотность распределения – унимодальная и симметричная функция, похожая на нормальное распределение, рис. 3.7.
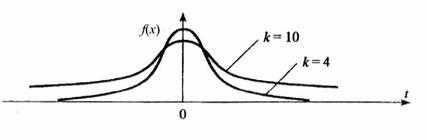
Рис. 3.7. Плотность распределения Стьюдента
Область изменения аргумента t от –∞ до ∞. Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2. По сравнению с нормальным распределение Стьюдента более пологое, оно имеет меньшую дисперсию. Это отличие заметно при небольших значениях k, что следует учитывать при проверке статистических гипотез (критические значения аргумента распределения Стьюдента превышают аналогичные показатели нормального распределения). Таблицы распределения содержат значения для односторонней (пределы интегрирования от r(k;a) до ∞.
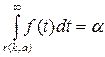
или двусторонней (пределы интегрирования от – r(k;a) до r(k;a))
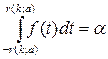
критической области.
Распределение Стьюдента применяется для описания ошибок выборки при k < 30. При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность
Р{t > t(k; a)} = u1– a(0, k/(k–2)),
где u1– a(0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.
Дата добавления: 2022-02-05; просмотров: 401;











