ТИПОВЫЕ РАСПРЕДЕЛЕНИЯ
При проверке гипотез широкое применение находит ряд теоретических законов распределения. Наиболее важным из них является нормальное распределение. С ним связаны распределения χ2 (хи-квадрат), Стьюдента, Фишера, а также интеграл вероятностей. Для указанных законов функции распределения аналитически не представимы. Значения функций определяются по таблицам или с использованием стандартных процедур пакетов прикладных программ. Указанные таблицы обычно построены в целях удобства проверки статистических гипотез в ущерб теории распределений – они содержат не значения функций распределения, а критические значения аргумента z(α).
Для односторонней критической области z(α) = z1–a, т.е. критическое значение аргумента z(α)) соответствует квантили z1–a уровня 1– α, так как
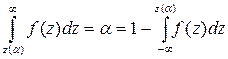 ,
,
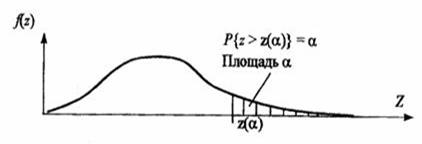
Рис. 3.3. Односторонняя критическая область
Для двусторонней критической области, с уровнем значимости α, размер левой области α2, правой α1 (α1+ α2= α), рис. 3.4. Значения z(α2) и z(α1) связаны с квантилями распределения соотношениями
z(α1)=z1–a1, z(a2)=za2,
так как
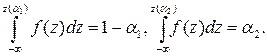
Для симметричной функции плотности распределения f(z) критическую область выбирают из условия a1=a2=a/2 (обеспечивается наибольшая мощность критерия). В таком случае левая и правая границы будут равны |z(a/2)|.
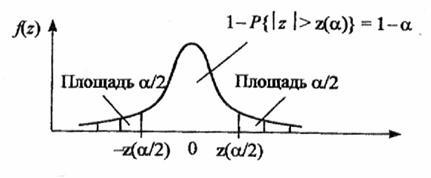
Рис. 3.4. Двусторонняя критическая область
Дата добавления: 2022-02-05; просмотров: 373;











