Критерий А.Н. Колмогорова

Для применения критерия А.Н. Колмогорова ЭД требуется представить в виде вариационного ряда (ЭД недопустимо объединять в разряды). В качестве меры расхождения между теоретической F(x) и эмпирической F*_n(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разности

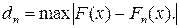(3.12)

А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины d_n асимптотически приближается к функции распределения

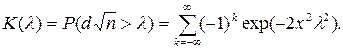
Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина d_n не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия

в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и F*_n(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.

1. В соответствии с условиями его применения необходимо пользоваться следующим соотношением

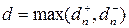
где

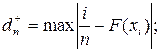
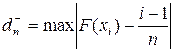
2. Условия применения критерия предусматривают, что теоретическая функция распределения известна полностью – известны вид функции и значения ее параметров. На практике параметры обычно неизвестны и оцениваются по ЭД. Но критерий не учитывает уменьшение числа степеней свободы при оценке параметров распределения по исходной выборке. Это приводит к завышению значения вероятности соблюдения нулевой гипотезы, т.е. повышается риск принять в качестве правдоподобной гипотезу, которая плохо согласуется с ЭД (повышается вероятность совершить ошибку второго рода). В качестве меры противодействия такому выводу следует увеличить уровень значимости a, приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.

Последовательность действий при проверке гипотезы следующая.

1. Построить вариационный ряд.

2. Построить график эмпирической функции распределения F*(x).

3. Выдвинуть гипотезу:

H0: F(x) = F0(x) ,

H1: F(x) F0(x) ,

где F0(x) - теоретическая функция распределения типового закона: равномерного, экспоненциального или нормального. Ниже приведены формулы для расчета F0(x).

Равномерный закон

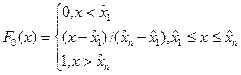
Экспоненциальный закон

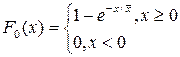
Нормальный закон

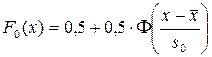
4. Рассчитать по формулам 10-20 значений и построить зависимость функции F0(x) в одной системе координат с функцией F*_n(x).

5. По графику определить максимальное по модулю отклонение между функциями F*_n(x) и F0(x).

6. Вычислить значение критерия

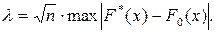
7. Принимают тот или иной уровень значимости (чаще всего 0,05 или 0,01). Тогда доверительная вероятность = 1 - .

8. Из таблицы вероятностей Колмогорова выбрать критическое значение .

9. Если > , то нулевая гипотеза H0отклоняется, в противном случае - принимается, хотя она может быть неверна.

Достоинства критерия Колмогорова по сравнению с критерием 2: возможность применения при очень маленьких объемах выборки (n < 20) , более высокая "чувствительность", а следовательно, меньшая трудоемкость вычислений.

Недостаток: критерий можно использовать в том случае, если параметры Q1, ..., Qkраспределения заранее известны, а эмпирическая функция распреде­ления F*(x) должна быть построена по несгруппированным выборочным данным.

Пример 3.3. По критерию Колмогорова проверить гипотезу о равно­мерном законе распределения R(0,5; 5,25) случайной величины по выборке объема 10: 2,68 1,83 2,90 1,03 0,90 4,07 5,05 0,94 0,71 1,16, уровень значимости 0,5.

Решение. Вариационный ряд данной выборки имеет вид:

0,71 0,90 0,94 1,03 1,16 1,83 2,68 2,90 4,07 5,05.

После этого строим график эмпирической функции распределения F*(x).

Теоретическая функция распределения F0(x) равномерного закона R(0,5;5,25) равна

.

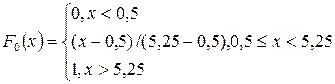Максимальная разность по модулю между графиками F*(x) и F0(x) равна 0,36 при х = 1,16.

Вычислим значение статистики

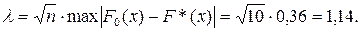
Из таблицы Колмогорова выбираем критическое значение 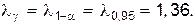Так как < 1,36 , то гипотеза о равномерном законе распределения принимается.

Критерий Р. Мизеса

В качестве меры различия теоретической функции распределения F(x) и эмпирической F*_n(x) по критерию Мизеса (критерию w²) выступает средний квадрат отклонений по всем значениям аргумента x

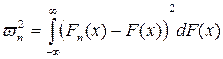. (3.12)

Статистика критерия

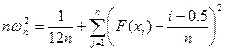(3.13)

При неограниченном увеличении n существует предельное распределение статистики nw_n². Задав значение вероятности a можно определить критические значения nw_n²(a). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nw_n² окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a гипотеза Но о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.

Пример 3.3. Проверить с помощью критерия Мизеса гипотезу о том, что ЭД, представленные вариационным рядом в табл. подчиняются нормальному распределению при уровне значимости a = 0,1.

Решение. Исходные данные и результаты вычислений представлены в табл. 3.1.

В этой таблице:

F_n(x_i)=(i–0,5)/44 – значение эмпирической функции распределения;

F(x_i) – значение теоретической функции распределения, соответствует значению функции нормального распределения в точке x_i;

D_i =1000[F_n(x_i) – F(x_i)]² . Здесь масштабный множитель 1000 введен для удобства отображения данных в таблице, при расчетах он не используется.

Критическое значение статистики критерия Мизеса при заданном уровне значимости равно 0,347, (таблица приведена в приложении в разделе «Практика»). Фактическое значение статистики

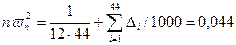
что меньше критического значения. Следовательно, гипотеза Н₀ не противоречит имеющимся данным.

Достоинством критерия Мизеса является быстрая сходимость к предельному закону, для этого достаточно не менее 40 наблюдений в области часто используемых на практике больших значений nw_n (а не несколько сот, как для критерия хи-квадрат).

Сопоставляя возможности различных критериев, необходимо отметить следующие особенности. Критерий Пирсона устойчив к отдельным случайным ошибкам в ЭД. Однако его применение требует группирования данных по интервалам, выбор которых относительно произволен и подвержен противоречивым рекомендациям. Критерий Колмогорова слабо чувствителен к виду закона распределения и подвержен влиянию помех в исходной выборке, но прост в применении. Критерий Мизеса имеет ряд общих свойств с критерием Колмогорова: оба основаны непосредственно на результатах наблюдения и не требуют построения статистического ряда, что повышает объективность выводов; оба не учитывают уменьшение числа степеней свободы при определении параметров распределения по выборке, а это ведет к риску принятия ошибочной гипотезы. Их предпочтительно применять в тех случаях, когда параметры закона распределения известны априори, например, при проверке датчиков случайных чисел.

При проверке гипотез о законе распределения следует помнить, что слишком хорошее совпадение с выбранным законом распределения может быть обусловлено некачественным экспериментом («подчистка» ЭД) или предвзятой предварительной обработкой результатов (некоторые результаты отбрасываются или округляются).

Выбор критерия проверки гипотезы относительно произволен. Разные критерии могут давать различные выводы о справедливости гипотезы, окончательное заключение в таком случае принимается на основе неформальных соображений. Точно также нет однозначных рекомендаций по выбору уровня значимости.

Рассмотренный подход к проверке гипотез, основанный на применении специальных таблиц критических точек распределения, сложился в эпоху "ручной" обработки ЭД, когда наличие таких таблиц существенно снижало трудоемкость вычислений. В настоящее время математические пакеты включают процедуры вычисления стандартных функций распределений, что позволяет отказаться от использования таблиц, но может потребовать изменения правил проверки. Например, соблюдению гипотезы Н₀ соответствует такое значение функции распределения критерия, которое не превышает значение доверительной вероятности 1– a (оценка статистики критерия соответствует доверительному интервалу).