СУЩНОСТЬ ЗАДАЧИ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.
Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.
Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если λ является параметром экспоненциального распределения, то гипотеза Н0 о равенстве λ =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве λ >10 состоит из бесконечного множества простых гипотез Н0 о равенстве λ =bi , где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.
Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки
z=z(x1, x2, …, xn).
Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.
Принятие или отклонение гипотезы Н0 по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок.
Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1.
Ошибка второго рода возникает с вероятностью β в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1.
Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0.
Вероятность отвергнуть ложную гипотезу Н0 называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1.
Таблица 3.1.
| Гипотеза H0 | Решение | Вероятность | примечание |
| Верна | Принимается | 1-α | Доверительная вероятность |
| Отвергается | α | Вероятность ошибки первого рада | |
| Неверна | Принимается | b | Вероятность ошибки второго рода |
| Отвергается | 1-b | Мощность критерия |
Например, рассмотрим случай, когда некоторая несмещенная оценка параметра Θ* вычислена по выборке объема n, и эта оценка имеет плотность распределения f(Θ*), рис. 3.1.
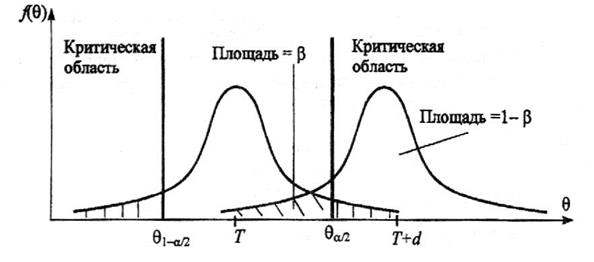 Рис. 3.1 Области принятия и отклонения гипотезы
Рис. 3.1 Области принятия и отклонения гипотезы
Предположим, что истинное значение оцениваемого параметра равно Θ. Если рассматривать гипотезу Н0 о равенстве Θ* =Θ, то насколько велико должно быть различие между Θ* и Θ, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между Θ* и Θ на основе выборочного распределения параметра Θ*.
Целесообразно полагать одинаковыми значения вероятности выхода параметра Θ* за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность того, что параметр Θ* выйдет за пределы интервала с границами Θ*1–a/2 иΘ*a/2, составляет величину α. Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства Θ* =Θ можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н0. Отсюда следует, что вероятность допустить ошибку первого рода равна  α (равна уровню значимости критерия).
α (равна уровню значимости критерия).
Если предположить, например, что истинное значение параметра в действительности равно Θ+d, то согласно гипотезе Н0 о равенстве Θ* =Θ – вероятность того, что оценка параметра Θ* попадет в область принятия гипотезы, составит b, рис. 3.2.
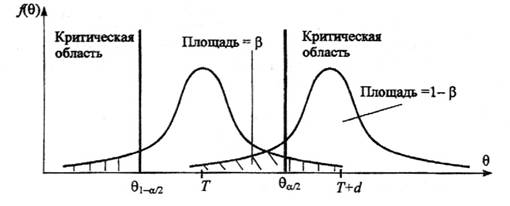
Рис.3.2. Области принятия и отклонения гипотезы
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости α. Однако при этом увеличивается вероятность ошибки второго рода b (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Θ – d.
Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность α была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения α относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами Θ*1–a/2 и Θ*a/2 для типовых значений α и различных способов построения критерия.
При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,3. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.
В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.
Дата добавления: 2022-02-05; просмотров: 439;











