Запись чисел в стандартном виде
Всякое положительное число можно записать в виде
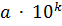 (*)
(*)
где число a удовлетворяет неравенствам 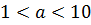 , k - целое число.
, k - целое число.
Если число записано в виде (*), то говорят, что оно записано в стандартном виде. Целое число k называется порядком данного числа.
Например, порядок числа 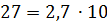 равен 1, порядок числа
равен 1, порядок числа 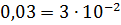 равен -2, порядок числа
равен -2, порядок числа 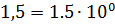 равен 0.
равен 0.
Например, если 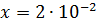 и
и 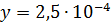 , то
, то 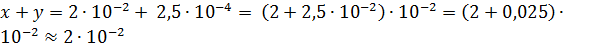
и следовательно, 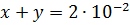 с точностью до
с точностью до 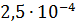 .
.
Аналогично, 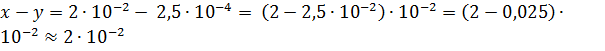 с точностью до
с точностью до 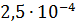 .
.
Если порядок числа x равен n, а порядок числа y равен m, то порядок произведения x∙y равен (n + m) или (n + m + 1).
Например, если 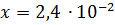 и
и 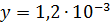 , тогда
, тогда 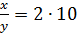 и
и 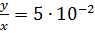 .
.
Погрешности простейших арифметических действий:
Положение 1. Предельная абсолютная погрешность суммы нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей слагаемых.
Замечание. При сложении приближенных чисел в полученном результате нужно отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из данных приближенных чисел.
Пример.Найти сумму 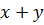 , если
, если  ,
, 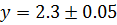
Решение: Из условия задачи следует, что 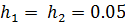 . По правилу подсчёта точности суммы получаем
. По правилу подсчёта точности суммы получаем 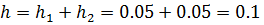 Следовательно,
Следовательно,  .
.
Положение 2.Предельная абсолютная погрешность разности двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
Замечание. При вычитании приближенных чисел в полученном результате нужно отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из данных приближенных чисел.
Пример. Найти разность  , если
, если 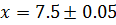 ,
, 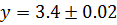
Решение: Из условия задачи следует, что 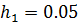 ,
, 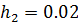 . По правилу подсчёта точности разности имеем
. По правилу подсчёта точности разности имеем 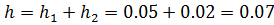 . Следовательно,
. Следовательно, 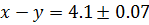 .
.
Положение 3. Предельная относительная погрешность произведения нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей сомножителей.
Замечание. При умножении приближенных чисел в результате нужно сохранять столько значащих цифр, сколько имеет приближенное данное с наименьшим количеством значащих цифр (самое «короткое» из данных приближенных чисел).
Пример. 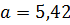 ;
; 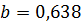 ;
; 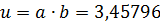
Решение: Будем иметь:
 ;
; 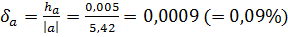 .
.
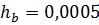 ;
;  .
.
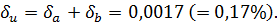
Но 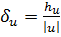 , откуда
, откуда 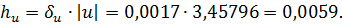
Если округлить число u до приближенного значения 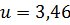 , то получим:
, то получим:
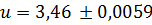 .
.
Положение 4.Предельная относительная погрешность от деления двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей делимого и делителя.
Замечание.При делении приближенных чисел в результате нужно сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр (самое «короткое» из данных приближенных чисел).
Пример. 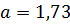 ;
; 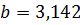 ;
; 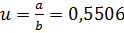
Решение: Будем иметь:
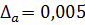 ;
; 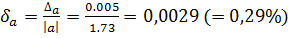 .
.
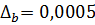 ;
; 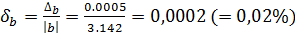 .
.
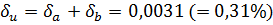 .
.
Но 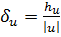 , откуда
, откуда 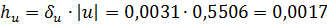 .
.
Если мы хотим округлить число u до приближенного значения 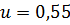 , то получим:
, то получим: 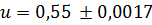 .
.
Положение 5. Предельная относительная погрешность степени приближенного числа, записанного в десятичной форме верными цифрами, равна произведению показателя степени на предельную относительную погрешность основания.
Замечание. При возведении приближенного числа в квадрат и куб в результате нужно сохранять столько значащих цифр, сколько их имеет возводимое в степень число.
Пример. Найти степень 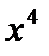 , если
, если 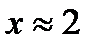 с точностью до 2.5%.
с точностью до 2.5%.
Решение: По правилу подсчёта точности степени получаем 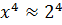 с точностью до
с точностью до 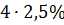 , т. е.
, т. е. 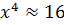 с точностью до 10%.
с точностью до 10%.
Найдём границу абсолютной погрешности степени: 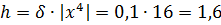 . Следовательно,
. Следовательно, 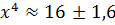 .
.
Положение 6. Предельная относительная погрешность корня из приближенного числа, записанного в десятичной форме верными цифрами, равна предельной относительной погрешности подкоренного числа, деленной на показатель корня.
Замечание. При извлечении квадратного или кубического корня из приближенного числа в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число.
Пример. Найти 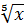 , если
, если 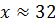 с точностью до 2.5%.
с точностью до 2.5%.
Решение: По правилу подсчёта точности корня получаем 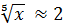 с точностью до
с точностью до 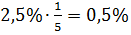 .
.
Найдём границу абсолютной погрешности степени: 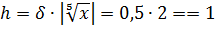 . Следовательно,
. Следовательно, 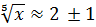 .
.
Лекция 14. МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Численное интегрирование – это вычисление определенного интеграла путем замены подынтегральной функции более простой аппроксимирующей функцией, последующего прямого интегрирования и получения расчетных формул (квадратурных формул).
Геометрический смысл определенного интеграла – это площадь криволинейной трапеции, описываемой подынтегральной функцией
Численные методы нахождения определенного интеграла сводятся к вычислению площади криволинейной трапеции путем замены y=f(x) более простой линией. В зависимости от того, многочленом какой степени заменяется кривая y=f(x), получают различные формулы численного интегрирования: формулы прямоугольников, формулу трапеции, формулу Симпсона.
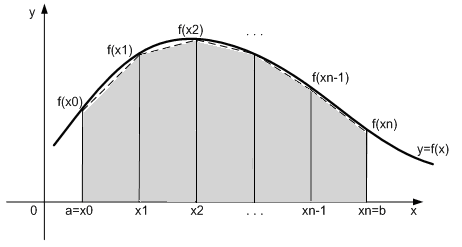
Рассмотрим график функции y=f(x) на [a;b]. Разобьем [a;b] точками на n равных частей, так что а=х0 < x1 < …< xn=b. Точки х0, х1,…хn – называют узлами разбиения.
Очевидно, что каждая точка 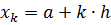 , где k = 1,2,…,n,
, где k = 1,2,…,n, 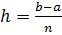 - шаг.
- шаг.
Формула средних прямоугольников:
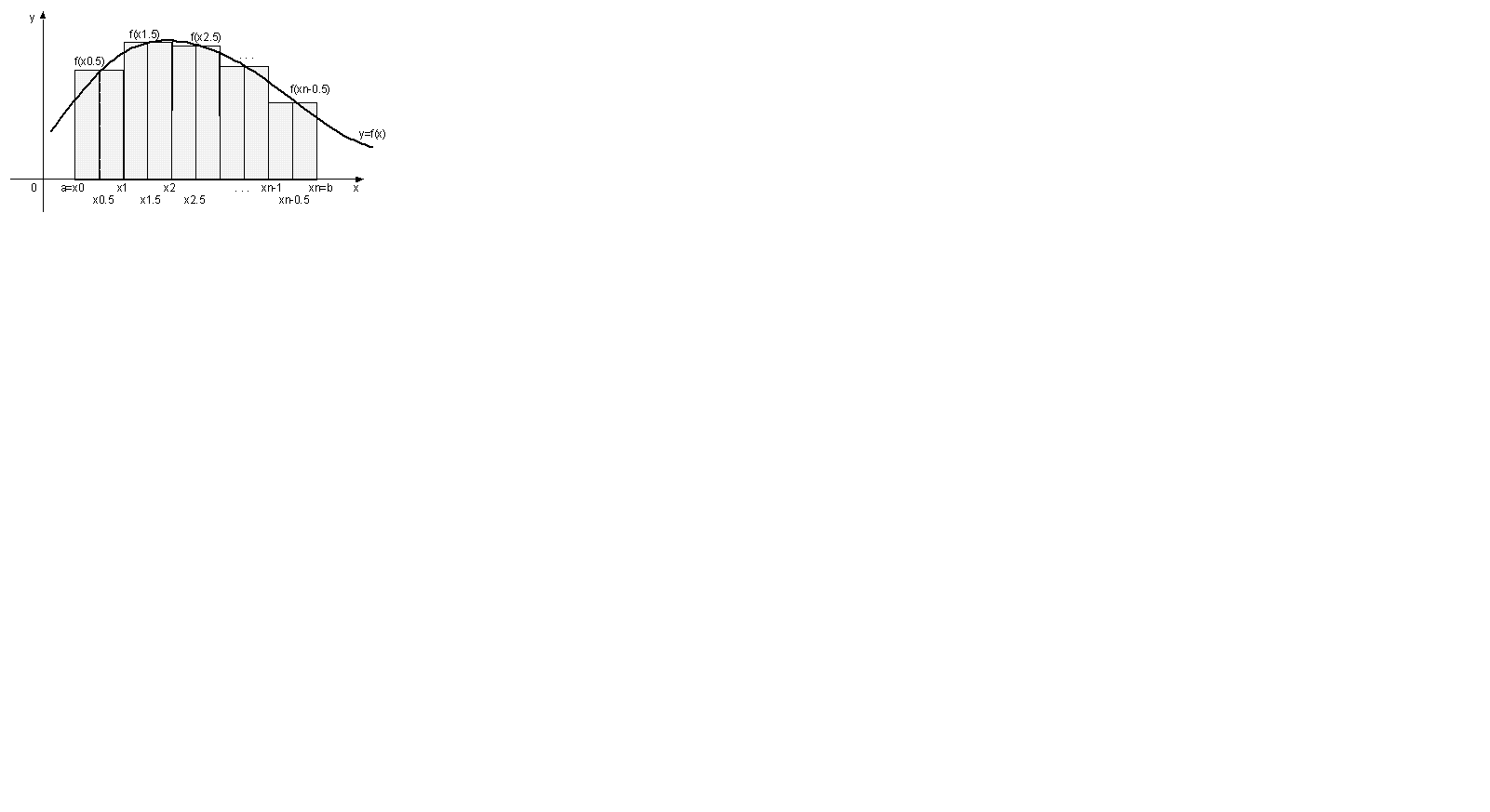
Формула средних прямоугольников для расчета:
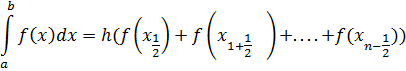
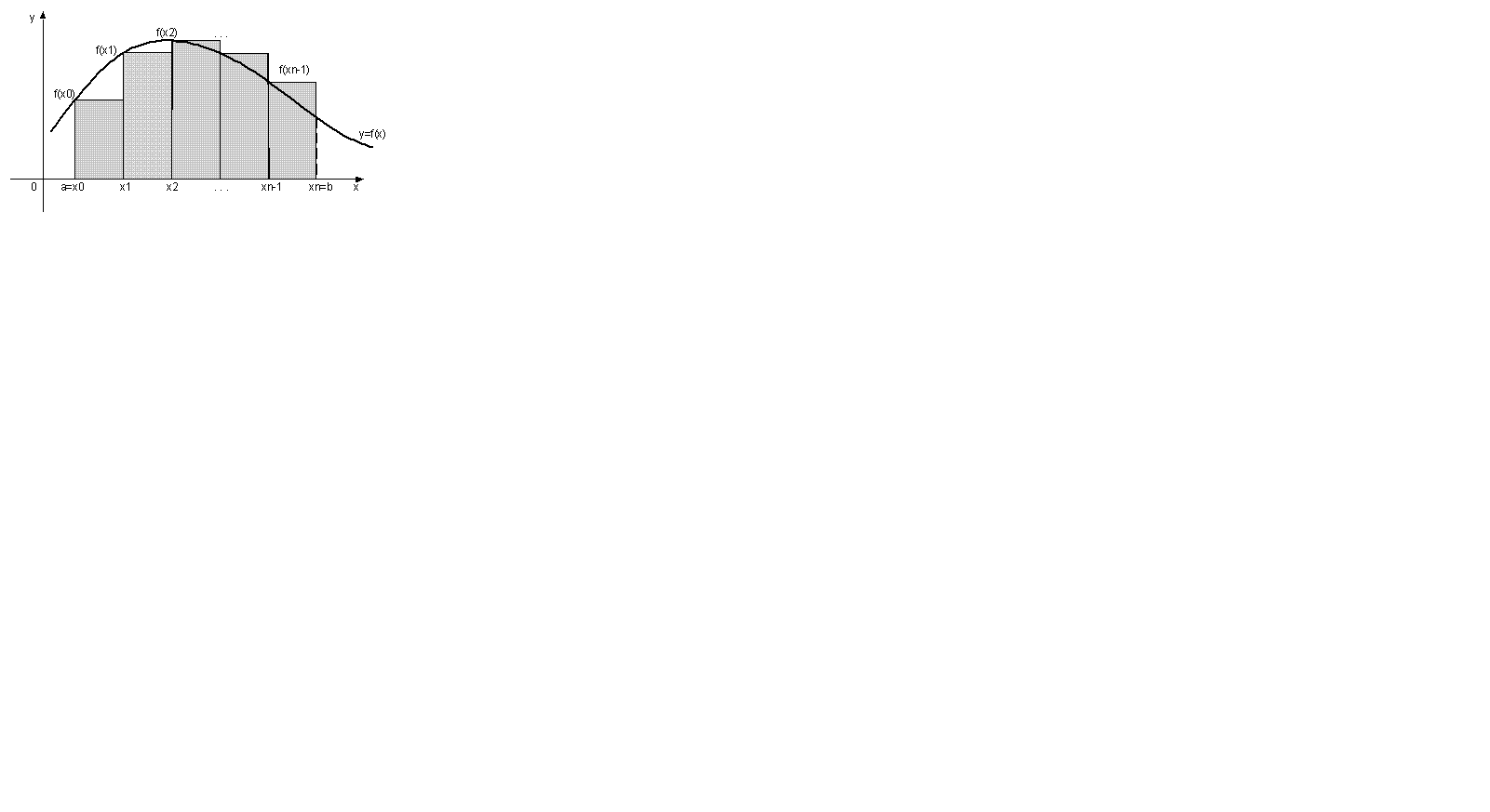 Формула левых прямоугольников:
Формула левых прямоугольников:
Формула для расчета:
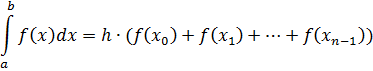
Формула правых прямоугольников:
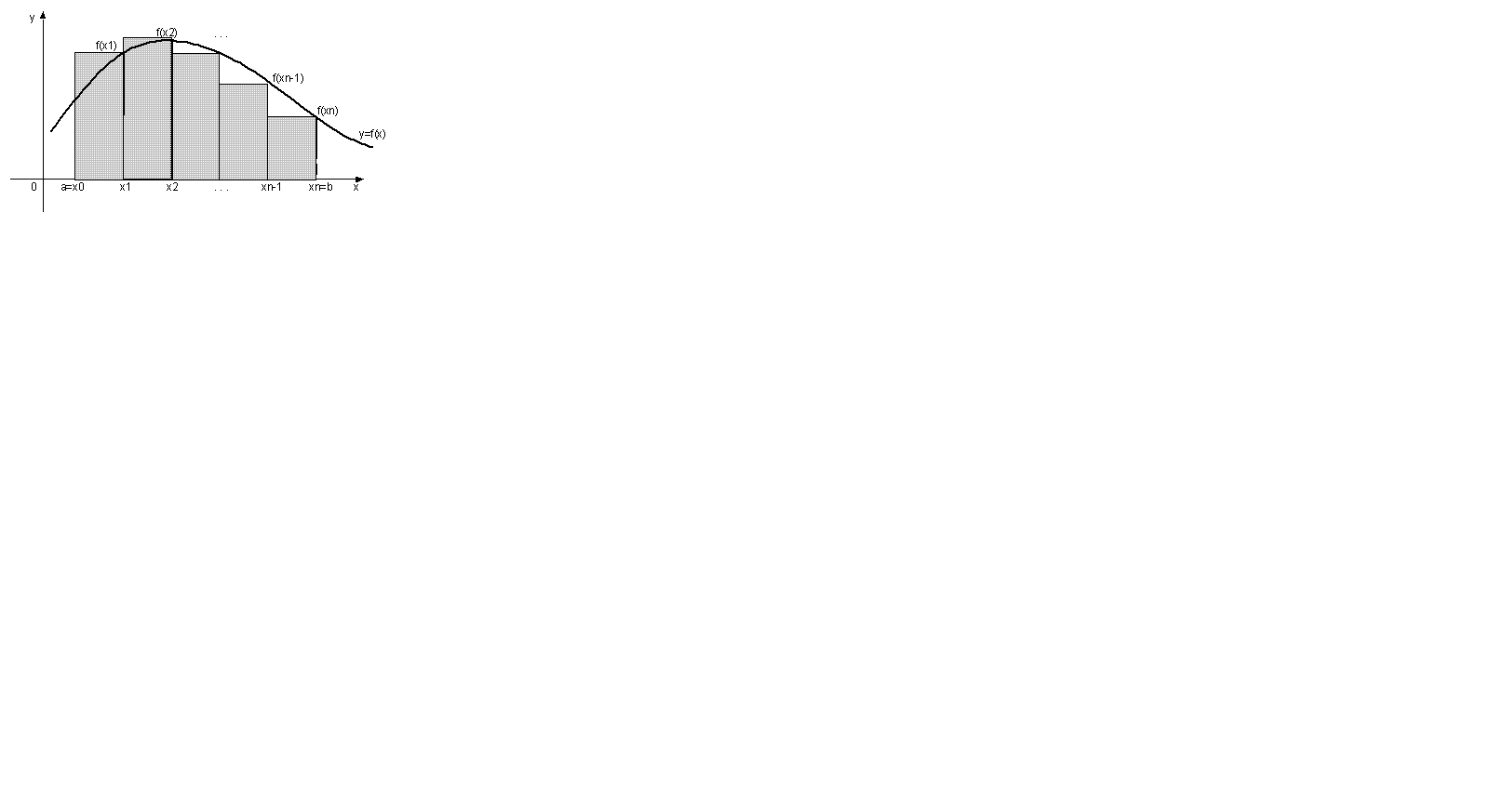
Формула для расчетов:
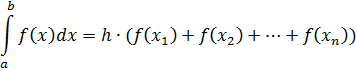
Формула трапеции:
Формула метода трапеции имеет вид:
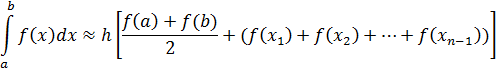
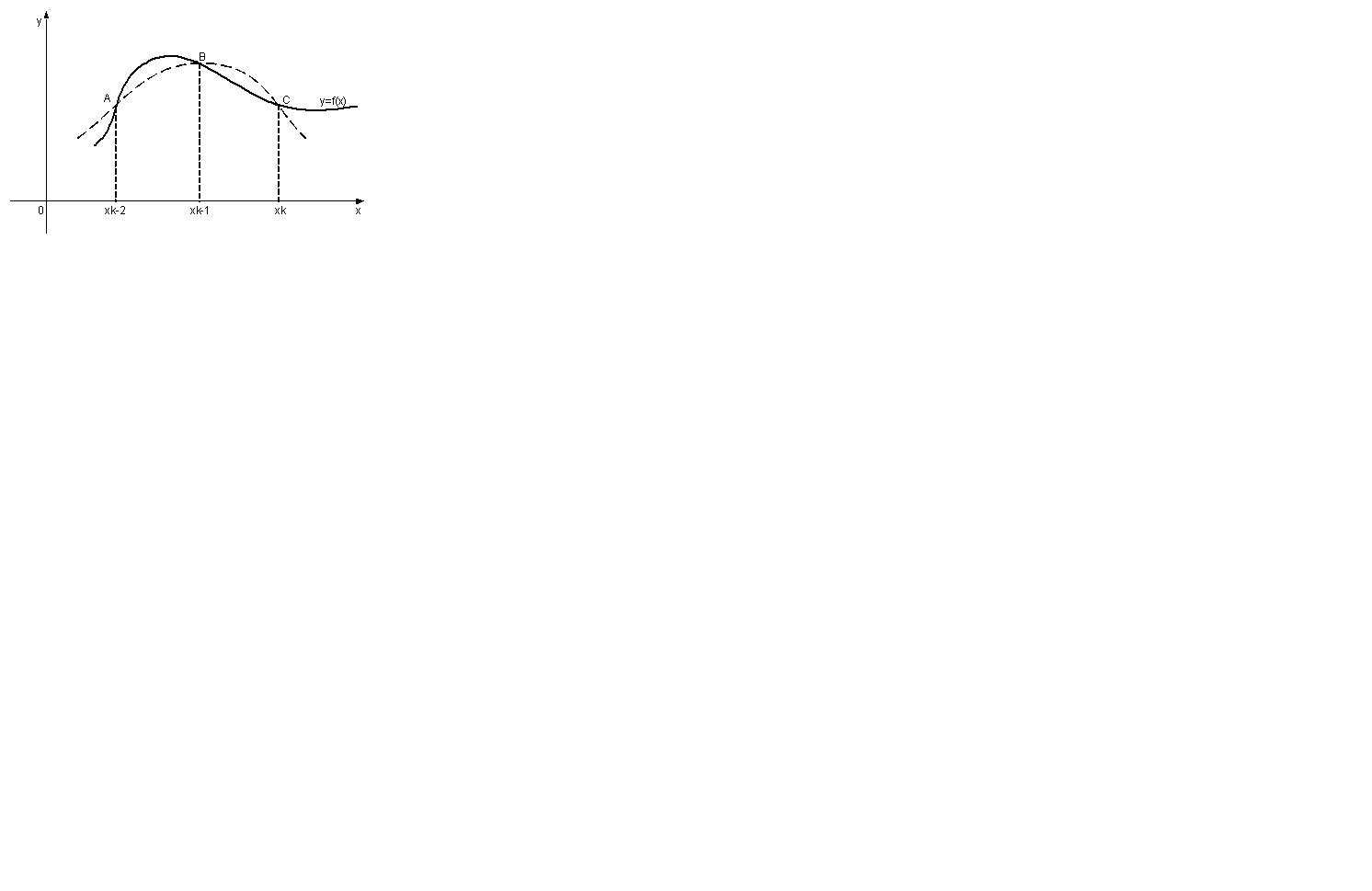 Метод Симпсона (метод парабол):
Метод Симпсона (метод парабол):
Формула для расчетов имеет вид:
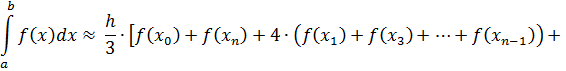
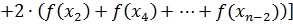
Пример.Вычислить определенный интеграл 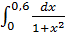 по формулам прямоугольников и трапеции при n=6,
по формулам прямоугольников и трапеции при n=6, 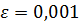 .
.
Решение: подынтегральная функция имеет вид f(x)= 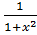 , a = 0, b = 0.6
, a = 0, b = 0.6
Шаг интегрирования равен 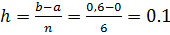
Так как 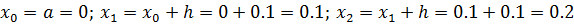 и т.д., то составим расчетную таблицу.
и т.д., то составим расчетную таблицу.
Примечание: в связи с тем, что определенный интеграл необходимо вычислить и по формуле средних прямоугольников, то шаг в таблице будет равен 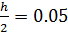 (см. таблицу)
(см. таблицу)
| n | xn | 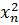
| 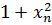
| f( xn)= 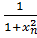
|
| 0,000 | 1,000 | 1,000 | ||
| 0,5 | 0,05 | 0,003 | 1,003 | 0,998 |
| 0,1 | 0,010 | 1,010 | 0,990 | |
| 1,5 | 0,15 | 0,023 | 1,023 | 0,978 |
| 0,2 | 0,040 | 1,040 | 0,962 | |
| 2,5 | 0,25 | 0,063 | 1,063 | 0,941 |
| 0,3 | 0,090 | 1,090 | 0,917 | |
| 3,5 | 0,35 | 0,123 | 1,123 | 0,891 |
| 0,4 | 0,160 | 1,160 | 0,862 | |
| 4,5 | 0,45 | 0,203 | 1,203 | 0,832 |
| 0,5 | 0,250 | 1,250 | 0,800 | |
| 5,5 | 0,55 | 0,303 | 1,303 | 0,768 |
| 0,6 | 0,360 | 1,360 | 0,735 |
Для вычисления определенного интеграла по формуле средних прямоугольников воспользуемся формулой:
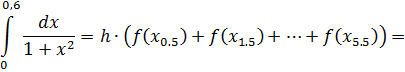
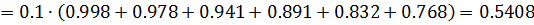
Для вычисления определенного интеграла по формуле левых прямоугольников воспользуемся формулой:
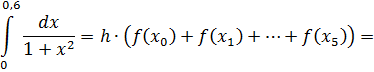
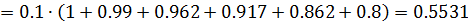
Для вычисления определенного интеграла по формуле правых прямоугольников воспользуемся формулой:
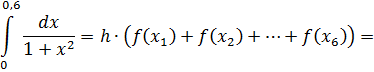
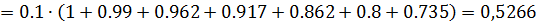
По формуле трапеции получим:
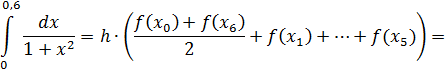
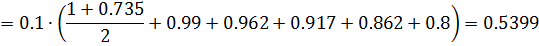
Дата добавления: 2016-06-05; просмотров: 4331;











