Сумма и произведение событий.

Два события А и В называются несовместными, если появление одного из них исключает возможность появления другого.

Два события А и В называются совместными, если появление одного из них не исключает возможность появления другого.

Суммой А + Вдвух событий А и В называется событие, состоящее в появлении либо события А, либо события В, либо обоих этих событий вместе.

Теорема.Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В)

Теорема. Вероятность суммы конечного или бесконечного множества несовместных событий равна сумме вероятностей этих событий:

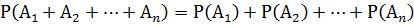
Следствие.Сумма вероятностей противоположных событий равна единице:

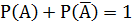или

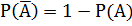
Пример. Студент сдает экзамен. Вероятность получить на экзамене «неуд» равна 0,1; «удовл.» - 0,6; «хорошо» - 0,2; «отл» - 0,1. Какова вероятность того, что студент получит на экзамене положительную оценку?

Решение:

Получить положительную оценку - это значит получить или «удовл.» или «хорошо» или «отл».

Р(А) = 0,6 – вероятность получить оценку «удовл.»;

Р(В) = 0,2 - вероятность получить оценку «хорошо»;

Р(С) = 0,1 - вероятность получить оценку «отл»;

Р(А) + Р(В) + Р(С) = 0,6 + 0,2 + 0,1 = 0,9.

Ответ: 0,9

Два события А и В называются независимыми, если вероятность появления одного события не зависит от того произошло другое событие или нет.

Вероятность произведения двух независимых событий равна:

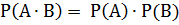
Пример.Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,7; вторым – 0,8; третьим – 0,9. Найти вероятность того, что 1) все три стрелка попадут в цель; 2) только два стрелка попадут в цель.

Решение:

Р(1) – вероятность того, что первый стрелок попадет в цель;

Р(2) – вероятность того, что второй стрелок попадет в цель;

Р(3) – вероятность того, что третий стрелок попадет в цель;

1)Соб.А – все три стрелка попадут в цель.

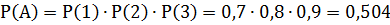
2)Соб. А - только два стрелка попадут в цель

Событие произойдет, если произойдет или событие 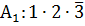или событие 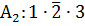или событие .

.

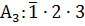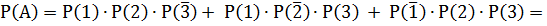
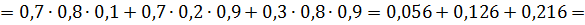
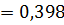Ответ:1)0,5042)0,398