Формула Тейлора для функции, не являющейся многочленом

Рассмотрим разложение основных функций в ряд Маклорена:

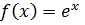· . Для любых действительных значений х функцию 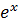можно представить в виде сходящегося ряда Маклорена

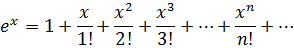
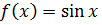· . Для любых действительных значений х функцию 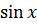можно представить в виде сходящегося ряда Маклорена

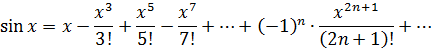
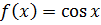· . Для любых действительных значений х функцию можно представить в виде сходящегося ряда Маклорена

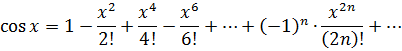
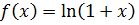· . Для любых действительных значений х функцию 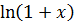можно представить в виде сходящегося ряда Маклорена

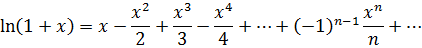
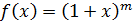· . Для любых действительных значений х функцию 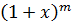можно представить в виде сходящегося ряда Маклорена

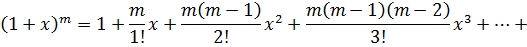
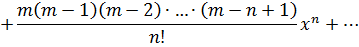
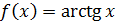· . Для любых действительных значений х функцию 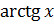можно представить в виде сходящегося ряда Маклорена

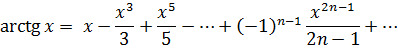
Пример. Разложить в ряд Маклорена следующие функции:

а)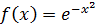

б)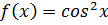

Решение:

а) воспользуемся формулой:

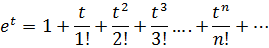
сделаем замену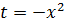

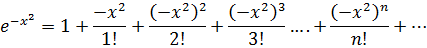
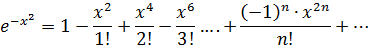
б) Воспользуемся известным соотношением из тригонометрии:

(*)

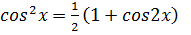Разложение функции имеет вид:

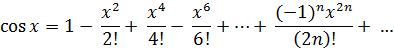
Заменим x в разложении cosx на 2x и получим разложение cos2x:

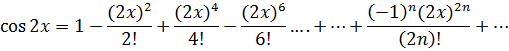
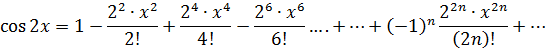
Найдем разложение :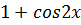

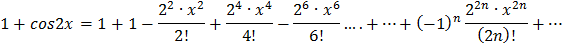
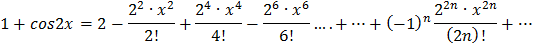
Тогда, разложение 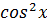будет иметь вид:

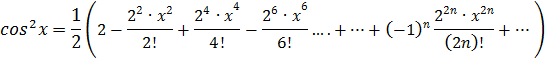
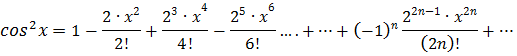
Лекция 11. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Комбинаторика

Комбинаторикой называется раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.

Правило суммы. Если некоторый объект А можно выбрать m способами, а объект В – k способами, то объект «либо А, либо В» («А или В») можно выбрать (m + k) способами.

Правило произведения. Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать k способами (независимо от выбора объекта А), то пары объектов можно выбрать А и В можно выбрать m∙k способами.

Выборки элементов

Пусть имеется некоторое множество из n элементов. Из этого множества можно образовать разные выборки, каждая из которых содержит m элементов (0 ≤ m ≤ n).

Выборка

УпорядоченнаяНеупорядоченная

- размещения (m ≠ n) - сочетания

- перестановки (m = n)

Размещениями с повторенияминазываются комбинации, составленные из n различных элементов по m элементов.

Характер выборки: 1) упорядоченная

2) с повторениями

Число размещений с повторениями:

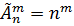
Размещениями без повторенийназывается комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.

Характер выборки: 1) упорядоченная

2) без повторений.

Число всех возможных размещений:

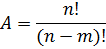
Перестановками без повторенийназываются комбинации, состоящие из одних и тех же n различных элементов и отличающихся только порядком их расположения.

Характер выборки: 1) упорядоченная

2) без повторений

Число всех возможных перестановок:

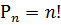
Перестановками с повторенияминазываются комбинации, в которых среди m элементов есть m₁ элементов одного вида, m₂ элементов другого вида и т.д., где m = m₁+ m₂+…+ m_k.

Характер выборки: 1) упорядоченная

2) без повторений

Число перестановок с повторениями:

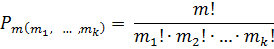
Сочетаниями без повторенийназываются комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.

Характер выборки: 1) неупорядоченная

2) без повторений

Число сочетаний из n элементов по m:

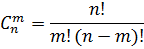
Сочетаниями с повторенияминазывается комбинации, составленные из n различных элементов по m элементов.

Характер выборки: 1) неупорядоченная

2) с повторениями.

Число сочетаний с повторениями:

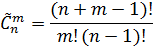
Пример. Сколько двухзначных чисел можно составить из нечетных цифр?

Решение: Определим сначала характер выборки:

1) упорядоченная (т.к. важен порядок цифр в числе)

2) с повторениями

Следовательно, это размещение с повторениями:

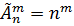
m=2, n=5, x={1,3,5,7,9}

.

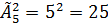Ответ: 25 чисел.

Пример.Сколько различных очередей можно составить из 8 человек?

Решение: Определим сначала характер выборки:

1) упорядоченная

2) без повторений

Следовательно, это перестановка без повторений. P_n= n!

n = 8

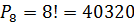
Ответ: 40320 очередей.

Пример.Сколько различных хорд можно провести через 6 точек, лежащие на окружности.

Решение: Определим сначала характер выборки :

1) неупорядоченная

2) без повторений

Следовательно, это сочетание без повторений.

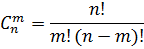
m=2, n=6.

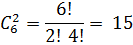
Ответ: 15 хорд.