Случайная величина. Числовые характеристики дискретной и непрерывной СВ.
Случайнойназывают величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной (прерывной) величиной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Законом распределения ДСВ называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| x | x1 | x2 | . . . | хn |
| р | p1 | p2 | . . . | pn |
при этом 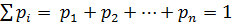
Числовые характеристики ДСВ:
1. Математическое ожидание:
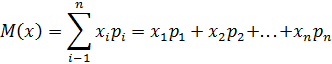
2. Дисперсия:
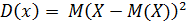 или
или 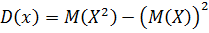
3. Среднее квадратическое отклонение:
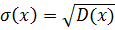
Непрерывной случайной величиной называют случайную величину у которой функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) вычисляется по формуле:
1 способ: 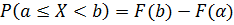 .
.
2 способ: 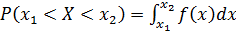
Плотностью распределения вероятности НСВ Х называют функцию f(x) - первую производную от функции распределения F(x):
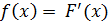
Числовые характеристики НСВ:
1. Математическим ожиданием НСВ Х:
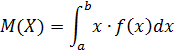
2. Дисперсия НСВ Х:
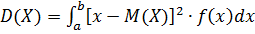 или
или 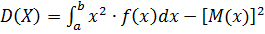
3. Среднее квадратическое отклонение НСВ Х:
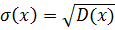
Пример. Задана ДСВ Х
| xi | |||
| pi | 0.3 | 0.4 | 0.3 |
Найти: 1) Функцию распределения F(х) ДСВ и построить ее график.
2) M(x), D(x), б(x).
Решение:
1) при x < 2
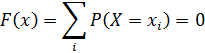
при 2 < x < 5
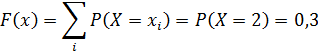
при 5 < x < 9
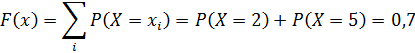
при x > 9
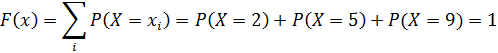
Тогда получим, 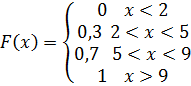
2) найдем числовые характеристики ДСВ:
а) 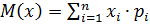 ;
;
M(x)=2 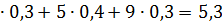
б) 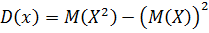 ;
;
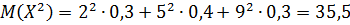
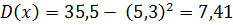
в) 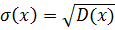
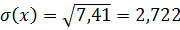
Пример. НСВ Х задана функцией распределения
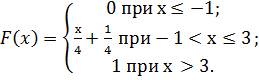
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,2).
Решение:
1способ:
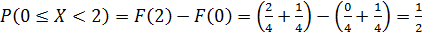 .
.
2 способ:
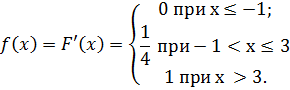
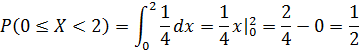
Ответ : 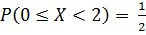 .
.
Пример. Найти математическое ожидание и дисперсию НСВ Х, заданной функции распределения
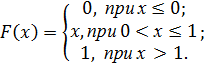
Решение:
Найдем функцию плотности распределения:
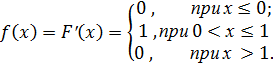
Найдем математическое ожидание по формуле:
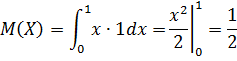
Найдем дисперсию по формуле:
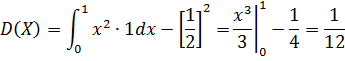
Лекция 12. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ
Необходимо заметить, что:
- любое измерение нельзя выполнить абсолютно точно: ошибку дает либо сам прибор, либо наблюдатель;
- счет дает точные результаты, только если количество пересчитываемых предметов невелико и если оно постоянно во времени;
- далеко не все математические операции можно выполнить абсолютно точно.
Поэтому первым в теории численных методов является вопрос о способах определения погрешности данного числа и о приемах определения погрешности чисел, полученных в результате ряда простейших арифметических действий с приближенными числами.
Величина 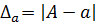 , где А – точное значение числа,
, где А – точное значение числа, 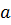 – его приближенное значение, называется абсолютной погрешностью числа
– его приближенное значение, называется абсолютной погрешностью числа 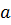 .
.
Границей абсолютной погрешности (ее предельным значением) называется возможно меньшее число 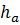 , про которое известно, что
, про которое известно, что 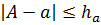 .
.
На практике мы вынуждены брать число 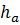 с запасом, так как точное значение А, как правило, остается неизвестным и, следовательно, невозможно вычислить
с запасом, так как точное значение А, как правило, остается неизвестным и, следовательно, невозможно вычислить 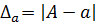 . Знание
. Знание 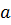 и
и 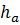 позволяет установить границы, в которых лежит точное число А, так как из неравенства
позволяет установить границы, в которых лежит точное число А, так как из неравенства 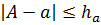 следует, что
следует, что 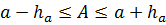 .
.
Например, запись 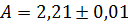 означает, что
означает, что 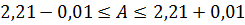 , или
, или 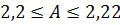 .
.
Замечание 1. Если 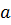 есть приближенное значение числа А, причем предельная абсолютная погрешность равна
есть приближенное значение числа А, причем предельная абсолютная погрешность равна 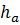 , то говорят, что
, то говорят, что 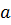 есть приближенное значение числа А с точностью до
есть приближенное значение числа А с точностью до 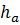 .
.
Замечание 2. Известно, что точное значение А некоторого числа находится в интервале 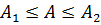 . Тогда, если его приближенное значение
. Тогда, если его приближенное значение 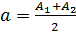 , то предельная абсолютная погрешность этого числа равна
, то предельная абсолютная погрешность этого числа равна 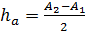 .
.
Пример. Известно, что 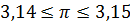 .
.
Если взять за приближенное значение числа 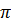 число
число 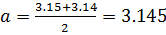 , то предельная абсолютная погрешность равна:
, то предельная абсолютная погрешность равна: 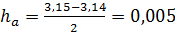 .
.
Таким образом, 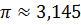 с точностью до 0,005.
с точностью до 0,005.
Однако абсолютная погрешность сама по себе не характеризует точности вычислений, поскольку она выражается в тех же единицах, что и измеряемая величина, и, следовательно, ее значение будет меняться, когда изменяются единицы, с помощью которых мы измеряем изучаемую величину.
Для характеристики точности приближенных вычислений вводят понятие относительной погрешности числа 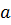 , являющегося приближенным значением величины А, которая определяется как отношение абсолютной погрешности к абсолютному значению числа
, являющегося приближенным значением величины А, которая определяется как отношение абсолютной погрешности к абсолютному значению числа 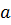 , т.е.
, т.е. 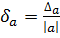 .
.
Границей относительной погрешности (ее предельным значением) будем называть возможно меньшее число 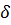 , про которое известно, что
, про которое известно, что
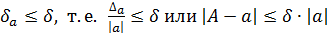 ,
,
откуда следует, что 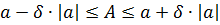 .
.
В отличие от абсолютной погрешности, относительная погрешность всегда величина безмерная, обычно выражаемая в процентах.
Пример.При измерении длины l и диаметра d некоторого провода получены значения 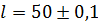 м,
м, 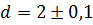 мм. Вычислить границы относительных погрешностей
мм. Вычислить границы относительных погрешностей 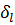 и
и 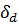 .
.
Решение:
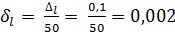 ,
, 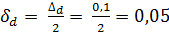
В процентах имеем: 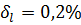 ,
, 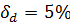
Лекция 13. ОКРУГЛЕНИЕ ЧИСЕЛ. ПОГРЕШНОСТИ ПРОСТЕЙШИХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Округлить число – значит сохранить в нем одну или несколько цифр, считая слева направо, а остальные отбросить.
Значащими цифрами приближенного числа называются все цифры в его записи начиная с первой ненулевой слева.
Цифра в представлении приближенного числа десятичной дробью называется верной, если абсолютная погрешность числа не превосходит единицы того разряда, в котором записана эта цифра. В противном случае она называется сомнительной.
Например, если а = 3,7412 ± 0,002 , то цифра 4 верная, так как 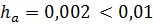 , следовательно, и предыдущие цифры 3 и 7 являются верными; цифра 1 сомнительная, так как
, следовательно, и предыдущие цифры 3 и 7 являются верными; цифра 1 сомнительная, так как 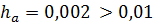 , следовательно и следующая цифра 2 является сомнительной.
, следовательно и следующая цифра 2 является сомнительной.
Правило (правило округления). Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если нужно для сохранения разрядов, заменяют их нулями.
При этом если первая из отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу.
Если же отбрасывается только одна цифра 5, то последнюю из сохраняемых цифр оставляют без изменения, если она четная, и увеличивают на единицу, если она нечетная.
Разряды десятичного числа:
| Х | Х | Х | Х | . | Х | Х | Х | Х |
| тысячи | сотни | десятки | единицы | десятые | сотые | тысячные | десятитысячные |
Пример: Округлить значение числа а = 145,7183 до единиц, сотых, тысячных, сотен.
Решение:
до единиц: а ≈ 146
до сотых: а ≈ 145,72
до тысячных: а ≈ 145,718
до сотен: а ≈ 100
Дата добавления: 2016-06-05; просмотров: 6837;











