Дифференциал функции
Дифференциалом функции 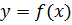 называется линейная часть приращения функции
называется линейная часть приращения функции 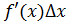 , которая отличается от приращения
, которая отличается от приращения 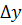 на бесконечно малую величину
на бесконечно малую величину 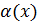 более высокого порядка, чем
более высокого порядка, чем 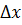 , и обозначается
, и обозначается 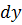 .
.
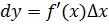 .
.
Таким образом, зная производную функции, можно найти ее дифференциал по формуле 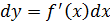 и, обратно, зная дифференциал функции, можно найти ее производную по формуле
и, обратно, зная дифференциал функции, можно найти ее производную по формуле
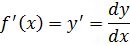
Пример. Найти дифференциал функции 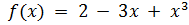
Решение:
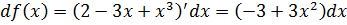 .
.
Формулы дифференцирования:
| Элементарных функций | Сложных функций |
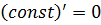
| |
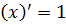
| |
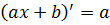
| |
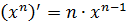
| 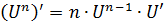
|
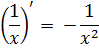
| 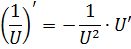
|
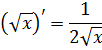
| 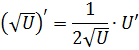
|
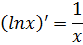
| 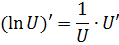
|
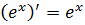
| 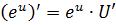
|
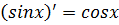
| 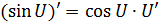
|
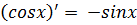
| 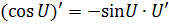
|
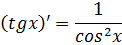
| 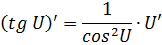
|
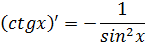
| 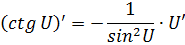
|
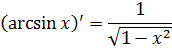
| 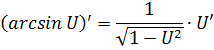
|
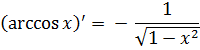
| 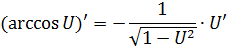
|
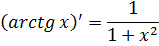
| 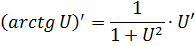
|
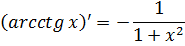
| 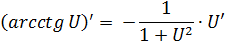
|
Лекция 7. Исследование функции с помощью производной
Признак монотонности функции:
Если для любых x1, х2 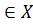 из условия x1< х2 следует неравенство f(x1)<f( х2) ( f(x1)>f( х2)), то функция называется возрастающей (убывающей) на промежутке
из условия x1< х2 следует неравенство f(x1)<f( х2) ( f(x1)>f( х2)), то функция называется возрастающей (убывающей) на промежутке 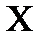 .
.
Рис.7.1. Возрастающая функция Рис.7.2. Убывающая функция
Теорема 1.Для того чтобы дифференцируемая функция 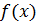 была возрастающей на интервале
была возрастающей на интервале 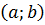 , достаточно, чтобы во всех точках
, достаточно, чтобы во всех точках 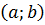 выполнялось равенство:
выполнялось равенство: 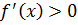
Теорема 2.Для того чтобы дифференцируемая функция 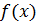 была убывающей на интервале
была убывающей на интервале 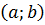 , достаточно, чтобы во всех точках
, достаточно, чтобы во всех точках 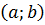 выполнялось равенство:
выполнялось равенство: 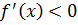
Отыскание точек локального экстремума функции:
Точка x0 называется точкой строгого локального максимума (минимума) функции f(x), если существует некоторая окрестность этой точки, в которой для всех x выполняется неравенство 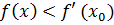
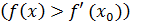 при
при 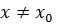 .
.
Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум.
Теорема 3 (необходимое условие локального экстремума).Если функция f(x) имеет в точке 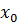 локальный экстремум и дифференцируема в этой точке, то f(x0)=0.
локальный экстремум и дифференцируема в этой точке, то f(x0)=0.
Точки, в которых производная функции равна нулю, принято называть точками возможного экстремума (стационарные точки).
Теорема 4 (достаточное условие локального экстремума).Пусть функция f(x) дифференцируема в некоторой окрестности точки x0. Тогда если f '(x) при переходе через точку x0 меняет знак с «+» на «-», то x0 - точка локального максимума, если f '(x) в точке x0 меняет знак с «-» на «+», то 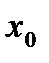 - точка локального минимума, если же знак f '(x) в точке x0 не изменяется, то в точке
- точка локального минимума, если же знак f '(x) в точке x0 не изменяется, то в точке 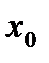 экстремума не существует.
экстремума не существует.
Направление выпуклости и точки перегиба графика функции:
График функции f '(x) имеет на интервале (a, b) выпуклость, направленную вниз (вверх), если в пределах интервала (a, b) график лежит не ниже (не выше) любой касательной к графику функции на (a, b).
Теорема 5.Если функция f '(x) имеет на интервале (a, b) вторую производную и 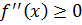
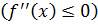 во всех точках (a, b), то график функции имеет на (a, b) выпуклость, направленную вниз (вверх).
во всех точках (a, b), то график функции имеет на (a, b) выпуклость, направленную вниз (вверх).
Точка M(x0; f(x0)) называется точкой перегибаграфика функции f '(x),если в точке М график имеет касательную и существует такая окрестность точки x0, в пределах которого график функции слева и справа от точки x0 имеет разные направления выпуклости.
Теорема 6 (необходимое условие точки перегиба).Пусть график функции f '(x) имеет перегиб в точке M(x0; f(x0)) и пусть функция имеет в точке 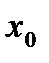 непрерывную вторую производную. Тогда f"(x0) в точке x0 обращается в нуль, т.е. f"(x0)=0.
непрерывную вторую производную. Тогда f"(x0) в точке x0 обращается в нуль, т.е. f"(x0)=0.
Точки M(x0; f(x0)) графика, для которых f"(x0)=0, называются критическими.
Теорема 7 (достаточное условие точки перегиба).Пусть функция 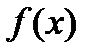 имеет вторую производную в некоторой окрестности точки
имеет вторую производную в некоторой окрестности точки 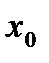 . Тогда если в пределах указанной окрестности
. Тогда если в пределах указанной окрестности 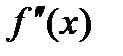 имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки 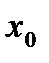 , то график функции имеет перегиб в точке М
, то график функции имеет перегиб в точке М 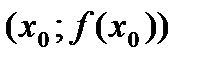 .
.
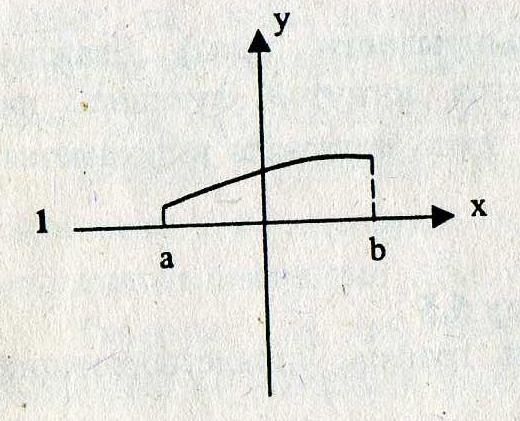 Пример:Указать, каким условиям удовлетворяет график функции.
Пример:Указать, каким условиям удовлетворяет график функции.
Решение:
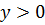 - график функции расположен выше оси ОХ
- график функции расположен выше оси ОХ
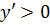 – график функции возрастает
– график функции возрастает
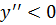 - график функции выпуклый
- график функции выпуклый
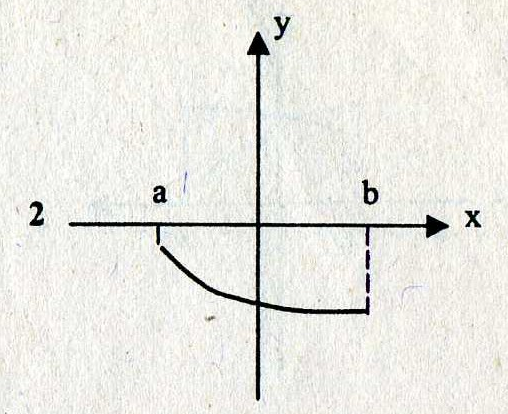
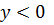 - график функции расположен ниже оси ОХ
- график функции расположен ниже оси ОХ
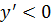 – график функции убывает
– график функции убывает
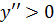 - график функции вогнутый
- график функции вогнутый
Пример:Исследовать функцию с помощью первой и второй производной.
y = 2 - 3x + x3
Решение:
1) D(f): x 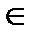 R
R
2) 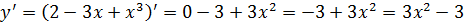
3) Исследуем функцию с помощью первой производной:
А) 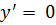 – приравниваем производную к нулю
– приравниваем производную к нулю
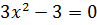
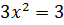
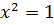
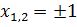 , тогда
, тогда 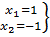 - критические точки первого рода
- критические точки первого рода
Б
| x |
| + |
| _ |
| + |
| -1 1 max min |
| Знак f ‘(x) Поведение f(x) Поведение f(x) |
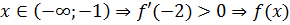 на этом интервале возрастает
на этом интервале возрастает
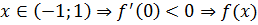 на этом интервале убывает
на этом интервале убывает
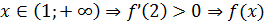 на этом интервале возрастает
на этом интервале возрастает
Т.к. при переходе через x1 = -1 производная меняет знак с «+» на «-»  x1 = -1 - точка максимума, а при переходе через x2 = 1 производная меняет знак с «-» на «+»
x1 = -1 - точка максимума, а при переходе через x2 = 1 производная меняет знак с «-» на «+»  x2 = 1 – точка минимума.
x2 = 1 – точка минимума.
Найдём значение функции в этих точках:
f max(-1) = 2-3(-1) + (-1)3 = 2 + 3 – 1 = 4
f min(1) = 2 - 3  1+13 = 2 – 3 + 1 = 0
1+13 = 2 – 3 + 1 = 0
Тогда, max(-1;4) ; min(1;0)
при 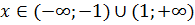 - функция возрастает
- функция возрастает
при x Î (-1;1) - функция убывает
4) Исследуем 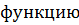 с помощью второй производной (на выпуклость, вогнутость и точки перегиба):
с помощью второй производной (на выпуклость, вогнутость и точки перегиба):
найдём 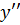 :
:
А) 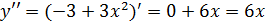
Б) приравняем 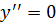 (вторую производную к нулю)
(вторую производную к нулю)
6x = 0
x = 0 - критическая точка второго рода
В) определим знаки второй производной на интервалах
| Знак f ‘’ (x) - + Поведение х f(x) 0 |
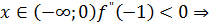 график выпуклый
график выпуклый
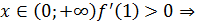 график вогнутый
график вогнутый
x = 0 – точка перегиба
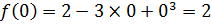
Тогда:
На интервале хÎ 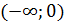 - график выпуклый
- график выпуклый
На интервале хÎ(0;+ 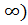 - график вогнутый
- график вогнутый
(0;2) - точка перегиба
5) Построим график данной функции: y = 2 - 3x + x3

Лекция 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ГЕОМЕТРИЧЕСКОЕ ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Дата добавления: 2016-06-05; просмотров: 3037;











