МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m×n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

, ,

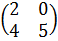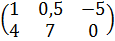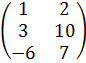
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

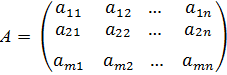
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами 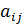: первый указывает номер строки, а второй – номер столбца.

Например, 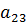– элемент стоит во 2-ой строке, 3-м столбце.

Виды матриц:

1. Квадратная – это матрица, у которой количество строк равно количеству столбцов. Число ее строк или столбцов называется порядком матрицы.

Например,

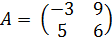- матрица второго порядка

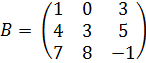- матрица третьего порядка

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Побочной диагональю квадратной матрицы назовём диагональ, идущую из левого нижнего в правый верхний угол.

Например, для матрицы

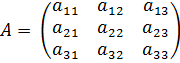
элементы 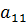, , 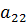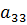- составляют главную диагональ;

элементы 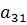, , 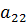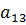- составляют побочную диагональ.

2. Прямоугольная – это матрица, в которой число строк не равно числу столбцов

3. Матрица, у которой всего одна строка называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

,

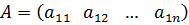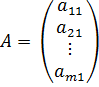
4. Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0.

5. Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

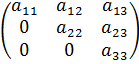
6. Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей.

Например,

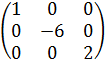
7. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E.

Например, единичная матрица 3-го порядка имеет вид

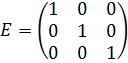
Лекция 2. ОПРЕДЕЛИТЕЛИ. СПОСОБЫ ВЫЧИСЛЕНИЯ

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом:

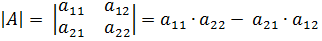
Определитель обозначается символом: 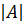, Δ.

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали.

Пример. Вычислить определители второго порядка.

А)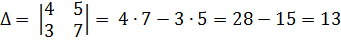

Б)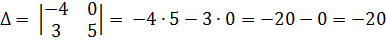

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

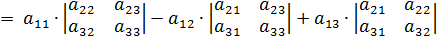
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Способы вычисления определителя третьего порядка:

1. Разложение по строке (или по столбцу).

Чтобы разложить определитель третьего порядка по строке или столбцу надо знать таблицу знаков:

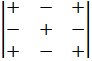
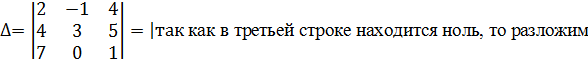
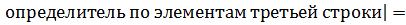
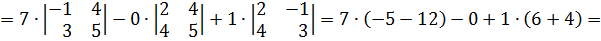
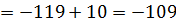
2. Метод Саррюса.

+ + + - - -

+ + + - - -

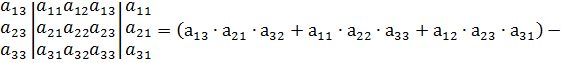
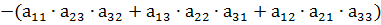
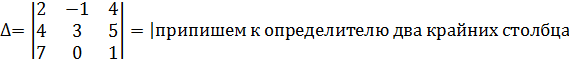
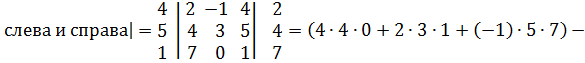
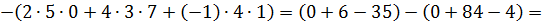
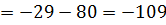
3. Метод треугольников.

=

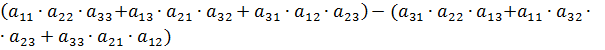
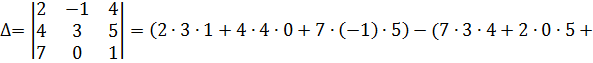
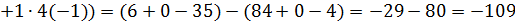
Лекция 3. СИСТЕМЫ ДВУХ (ТРЕХ) ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ (ТРЕМЯ) НЕИЗВЕСТНЫМИ. МЕТОД КРАМЕРА

3.1. Система вида

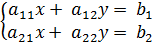
где х, у – неизвестные, 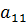, , 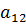, 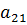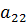- коэффициенты при неизвестных, 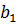, 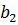- свободные члены

называется системой двух линейных уравнений с двумя неизвестными.

Решение системы двух линейных уравнений с двумя неизвестными методом Крамера.

Пусть имеется система уравнений:

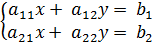
Обозначим через Δ главный определитель матрицы системы и через Δ_x и Δ_у определители, которые получаются из определителя Δ заметой 1-го (2-го) столбца столбцом из свободных членов.

; ;

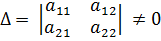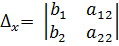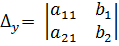
Тогда система имеет единственное решение, которое находится по формулам:

;

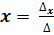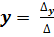
Пример. Решить систему методом Крамера.

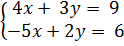
Решение:

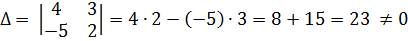
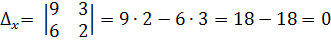
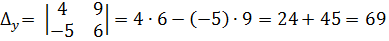
Тогда,

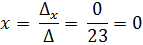
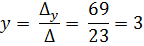
Ответ: х = 0, у = 3

3.2. Система вида

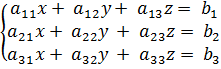
где х, у, z – неизвестные, 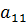, , 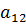, 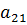. . . , 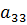- коэффициенты при неизвестных, 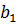, , 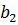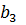- свободные члены

называется системой трех линейных уравнений с тремя неизвестными.

Решение системы трех линейных уравнений с тремя неизвестными методом Крамера.

Пусть имеется система уравнений:

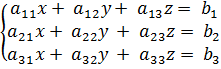
Обозначим через Δ главный определитель матрицы системы и через Δ_x , Δ_у и Δ_z определители, которые получаются из определителя Δ заметой 1-го, 2-го и 3-го столбцов столбцом из свободных членов.

; ;

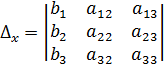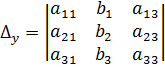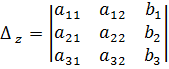
Тогда система имеет единственное решение, которое находится по формулам:

; ;

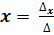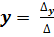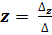
Пример. Решить систему методом Крамера.

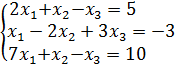
Решение:

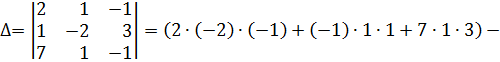
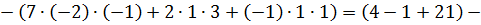
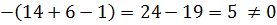
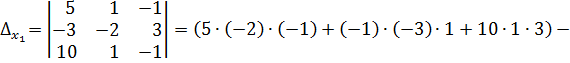
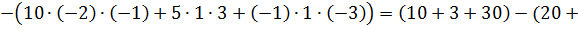
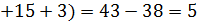
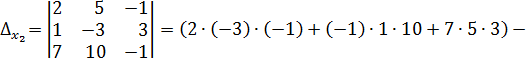
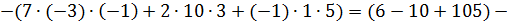
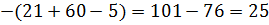
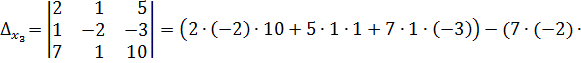
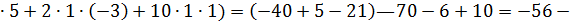
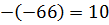
Тогда, ; ;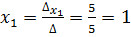

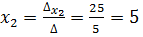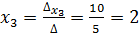
Ответ: х₁ = 1; х₂ = 5 ; х₃ = 2

Лекция 4. КОМПЛЕКСНЫЕ ЧИСЛА