Контрольные задания

Выполнить необходимые расчёты для построения аппроксимирующей функции вида

,

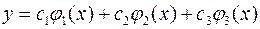которая описывает экспериментальные данные, приведённые на графиках в количестве 20-ти точек (см. рис.5–14).

Для построения аппроксимирующей функции выбрать три функции из четырёх j_i(x) (i = 1,2,3,4), заданных в таблице 1. График аппроксимирующей функции вместе с точками, описывающими экспериментальные данные вывести на экран монитора. Вывести на печать значения коэффициентов с₁, с₂ и с₃ и записать с ними аппроксимирующую функцию y.

При выполнении лабораторной необходимо перебрать все возможные варианты формирования аппроксимирующей функции из четырёх имеющихся функций (j₁ – j₂ – j₃, j₁ – j₂ – j₄, j₁ – j₃ – j₄ и j₂ – j₃ – j₄), привести в отчете результаты аппроксимации, которые они дают, и обосновать свой выбор лучшего варианта.

1-3. Диаграмма испытаний на растяжение цилиндрического об­разца из нержавеющей стали 1Х18Н9Т.	4-6. Диаграмма избыточного давления в цилиндре четырехтактного двигателя в зависимости от угла поворота его вала.
Рис.5.	Рис.6.

Рис.7.

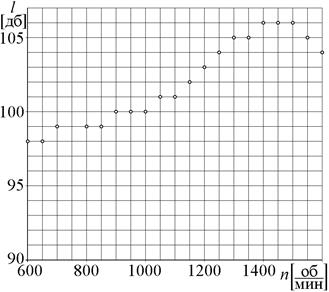
7-9. Степень обогащенности газовой смеси карбюратора в зависимости от перепада давления на его диффузоре.	10-12. Уровень шума работы дизельного двигателя Д.3–28/АТ в зависимости от числа оборотов вращения его вала.
Рис.7.	Рис.8.

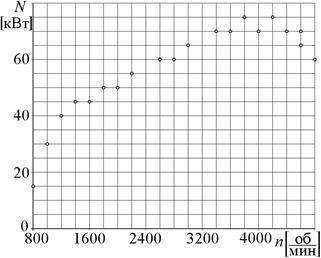
13-15. Зависимость мощности кар­бюраторного двигателя 11Ф–615 от числа оборотов вращения его вала.	16-18. Вертикальное смещение передней части кузова автомобиля при переезде единичной неровности на V = 50 км/час.
Рис.9.	Рис.10.

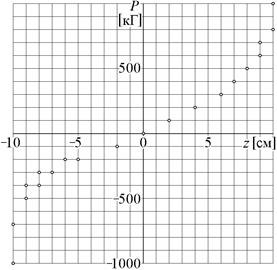
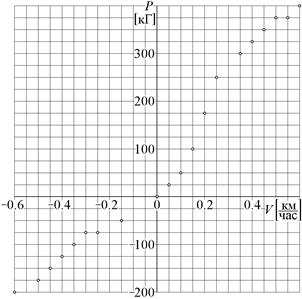
19-21. Зависимость амплитуды вертикальных колебаний передней части кузова автомобиля при переезде единичной неровности от скорости его движения.	22-24. Упругая характеристика независимой подвески McCon­nell передних колес легкового автомобиля 405 Station Wagon (Peugeot, 1933).
Рис.11.	Рис.12.

25-27. Перегрузка передней части кузова автомобиля в зависимости от частоты возбуждающей силы на подвеске передних колес.	28-30. Жёсткостная характеристика амортизатора подвески автомобиляScorpio 2.9i V6–24V GHIA (Ford, 1963).
Рис.13.	Рис.14.

Таблица 1. Варианты функций j₁(x), j₂(x), j₃(x) и j₄(x), составляющих аппроксимирующую функцию.

Варианты 1–3 (Рис.6, ε0= 0.2)
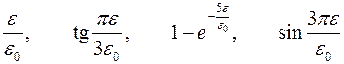
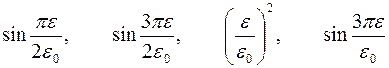
Варианты 4–6 (Рис.7, φ0= 30о)
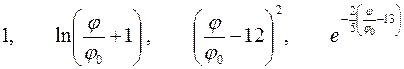
Варианты 7–9 (Рис.8, p0= 4 КПа)
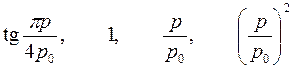
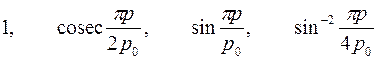
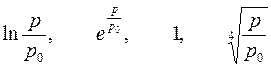
Варианты 10–12 (Рис.9, n0= 200 об/мин)

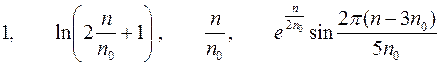
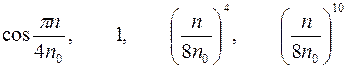
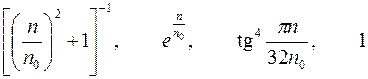
Таблица 1. Продолжение.

Варианты 13–15 (Рис.10, n0= 800 об/мин)
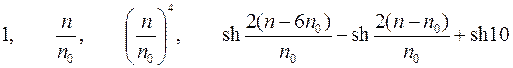
Варианты 16–17 (Рис.11, t0= 1.2 сек)
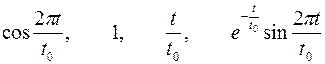
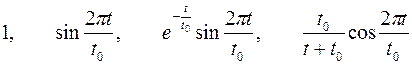
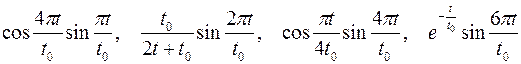
Варианты 19–21 (Рис.12, V0= 20 км/час)
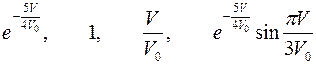
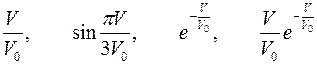
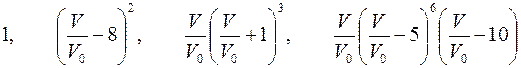
Варианты 22–24 (Рис.13, z0= 5 см)

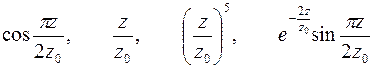
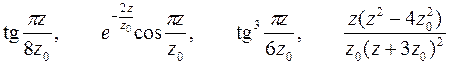
Таблица 1. Продолжение.

Варианты 25–27 (Рис.14, ω0= 10 Гц)
Варианты 28–30 (Рис.15, V0= 0.2 м/сек)

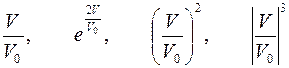
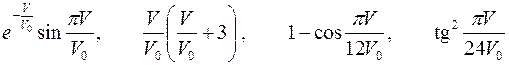
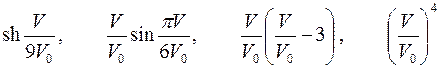
6. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-ГО ПОРЯДКА