Метод Гаусса с выбором главного элемента

Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего уравнения. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используетсяуравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца, i-ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй – по строке, а третий – по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения.

В качестве примера можно рассмотреть задачу отыскания решения следующей системы уравнений

при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения.

Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.

1. Прямой ход.

а. Выбор главного элемента среди элементов первого столбца

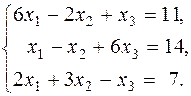
б. Нормировка первого уравнения

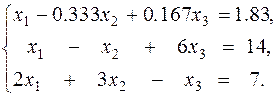
в. Исключение элементов первого столбца

г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений

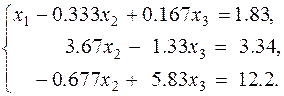
д. Нормировка второго уравнения

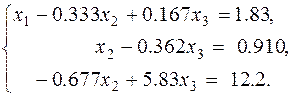
е. Исключение элементов второго столбца

ё. Нормировка последнего уравнения

2. Обратный ход

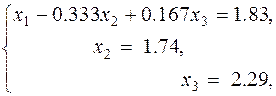
В итоге получено решение системы уравнений

.

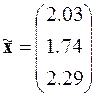3. Погрешность найденного решения.

а. Пересчёт вектора правых частей системы

.

б. Формирование системы уравнений, определяющей погрешности решения

,

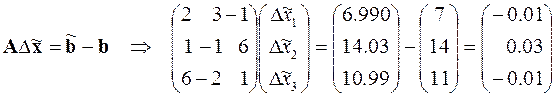то есть

.

в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей

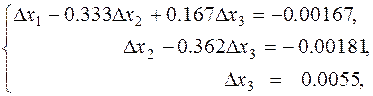
а обратный ход позволяет получить решение

.

г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений

,

,

.

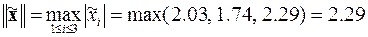Реализация описанного метода без нахождения погрешности решения в рамках программы Excel приведена на рис.1.

Рис.1.