Справочная информация

Интерполяцией называется приближение функции, значения которой заданы в виде таблицы, некоторой другой функцией, которая имеет аналитическое описание и которая совпадает с исходной при табличных значениях аргумента.

Простейшая задача, приводящая к интерполяции функций, заключается в следующем. В дискретные моменты времени x₁, x₂,..., x_n измеряется значение некоторой физической величины y, то есть наблюдается зависимость функции y от аргумента x, и строится таблица

По этой таблице требуется восстановить значения функции при любых других значениях аргумента x из отрезка [x₁, x_n] или подобрать аналитическое выражение для приближающей функции y(x) достаточно простого вида, значения которой совпадали бы с заданными в таблице

.

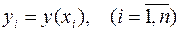Геометрический смысл задачи состоит в том, что через точки, которыми отображаются табличные значения аргумента и функции на поле декартовой системы координат x0y, как это показано на рис.1, и которые называются узловыми точками или узлами интерполяции, необходимо провести, по крайней мере, непрерывную линию, подобрав для неё аналитическое описание.

В зависимости от требований, которые накладываются на приближающую функцию, могут применяться различные формы её представления: линейная, квадратичная, кубическая или более высокого порядка. К простейшим из них относятся кусочно-линейная интерполяция, интерполяция кубическим сплайном и интерполяция многочленами, в частности, многочленом Лагранжа и другие.