Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 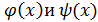 – это значит , найти предел их отношения при x
– это значит , найти предел их отношения при x 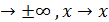 0.
0.
Пусть 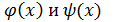 – б.м.функции.
– б.м.функции.
1. Функции 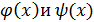 называются б. м. одного и того же порядка малости , если
называются б. м. одного и того же порядка малости , если 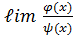 = c =const
= c =const 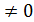 .
.
Пример.Сравнить функции: 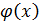 = x2-4 и
= x2-4 и 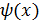 = x2-5x +6при x
= x2-5x +6при x 
Решение. 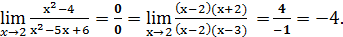
Вывод.Функции 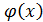
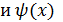 одного и того же порядка малости.
одного и того же порядка малости.
2. Функция 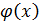 называется б.м. более высокого порядка малости чем
называется б.м. более высокого порядка малости чем 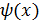 , если
, если 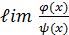 = 0.
= 0.
Пример.Сравнить функции 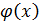 =
= 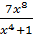 и
и 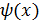 = x при x
= x при x 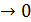 .
.
Решение. 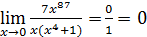 .
.
Вывод.Функция 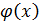 более высокого порядка малости чем функция
более высокого порядка малости чем функция 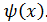
3. Функция 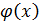 называется б.м. более низкого порядка малости чем
называется б.м. более низкого порядка малости чем 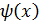 если
если
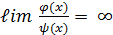 .
.
4. Функции 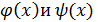 называются не сравнимыми ,если
называются не сравнимыми ,если 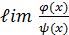 не существует. 69
не существует. 69
Пример.Пусть 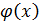 =
= 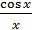 ,
, 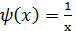 , x
, x 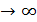 .
.
Решение. 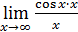 =
= 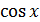 , не сущуствует.
, не сущуствует.
Вывод.Функции 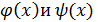 не сравнимы.
не сравнимы.
5. Две функции 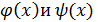 называются эквивалентными или равносильными , если
называются эквивалентными или равносильными , если 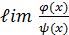 =1. Обозначается
=1. Обозначается 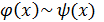
Пример.Вычислить 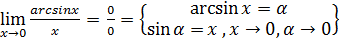 =
= 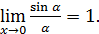
Вывод. arcsinx 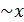

Можно показать , что arctg x 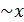 .
.
Составим таблицу эквивалентных функций: при x 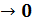
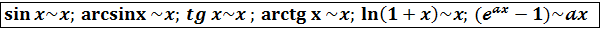
Теорема. Предел отношения 2-х б.м. функций равен пределу отношения эквивалентных им функций.
Доказательство. Пусть 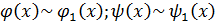 . Докажем , что
. Докажем , что 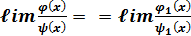 . Имеем
. Имеем 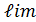
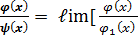
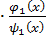

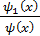 ]=
]= 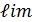
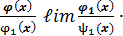
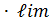
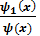 =
= 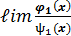 ч.т.д. 1
ч.т.д. 1
Замечание.Под знаком предела можно заменять функции им эквивалентными.
Примеры. Вычислить : 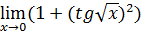 1/2x =
1/2x = 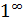 =
= 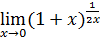 =
= 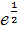 .
.
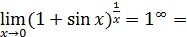
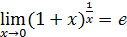 .
.
Дата добавления: 2016-06-05; просмотров: 4064;











