Лекция 24. Дифференциал функции.
Пусть функция y = f (x) дифференцируема на некотором интервале , тогда
Y’ = 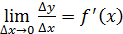 по теореме (
по теореме (  о пределе функции , имеем
о пределе функции , имеем
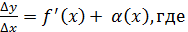
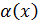 → б.м.функция , при
→ б.м.функция , при 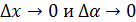 ,
,
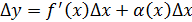 , f’(x)
, f’(x) 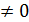 поэтому f’(x)
поэтому f’(x) 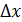 - б.м. 1-го порядка малости относительно
- б.м. 1-го порядка малости относительно 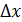 . Проверим , какого порядка малости
. Проверим , какого порядка малости 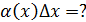 Найдём
Найдём 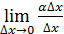 =
= 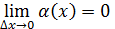 , то есть
, то есть 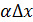 более высокого порядка малости , чем
более высокого порядка малости , чем 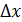 . 1- е слагаемое f’(x)
. 1- е слагаемое f’(x) 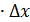 называется главной частью приращения функции.
называется главной частью приращения функции.
Определение. Дифференциалом функции называется главная часть приращения функции , линейная относительно 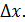
Обозначается 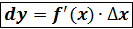 . Если y= f(x) = x , то y’x = 1 , а
. Если y= f(x) = x , то y’x = 1 , а 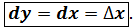
Вывод.Дифференциал независимой переменной равен приращению этой переменной 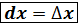 ,
, 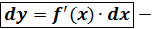 рабочая формула.
рабочая формула.
Пример .Найти дифференциал функции y = 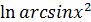 .
.
Решение.f’(x) = 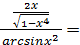
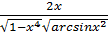 ,dy =
,dy = 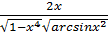 dx .
dx .
Приближённые вычисления с помощью дифференциала функции
Запишем приращение функции y = f(x) 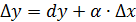 , так как последнее слагаемое более высокого порядка , то его отбросим и получим
, так как последнее слагаемое более высокого порядка , то его отбросим и получим 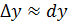 или
или
F (x0 + 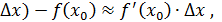 отсюда
отсюда 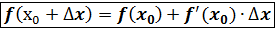 -формула для приближённого вычисления с помощью дифференциала функции.
-формула для приближённого вычисления с помощью дифференциала функции.
Пример. Вычислить sin 460 .
Решение. Пусть f(x) = sin x ; f’(x) = cos x ;sin(x+ 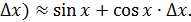
Примемx0 + 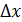 = 460 ; x0 =
= 460 ; x0 =  , тогда
, тогда 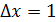 0 =
0 = 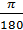
Sin460=sin ( 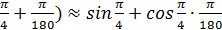 =
= 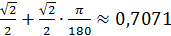 .
.
Ответ. Sin460 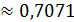 .
.
Дата добавления: 2016-06-05; просмотров: 1615;











