Способы задания функции
1. Аналитический – формулой. F (x) = 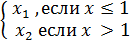
2. Табличный. Составляется таблица , в которой ряд значений x и y.
| x | 100 | 200 | 300 |
| Y | 1,6 | 1,8 |
3. Графический способ. 0 1 x y = 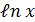
Определение.Элементарной называется функция , которую можно задать одним выражением , составленным из основных элементарных функций с помощью 4-х арифметических действий ( сложения, вычитания , умножения , деления).
Определение.Сложной функцией ( или функцией от функции ) y = f [ 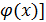 называется функция , определённая следующим образом: каждому x из области определения функции
называется функция , определённая следующим образом: каждому x из области определения функции 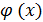 соответствует такое значение y , что y = f(u) , где u =
соответствует такое значение y , что y = f(u) , где u = 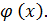 Переменная u называется промежуточным аргументом сложной функции. Например : y =
Переменная u называется промежуточным аргументом сложной функции. Например : y = 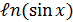 → y =
→ y = 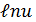 , где u = sinx .
, где u = sinx .
Определение.Функция y = f(x) называется чётной , если f(-x) = f(x). График такой функции симметричен относительно оси оy.
Определение.Функция y = f(x) называется нечётной, если f(-x) =- f(x) . График
нечётной функции симметричен относительно начала координат.
Определение.Функция x = 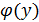 называется обратной для функции y = f(x) , если область определения функции y является областью изменения функции x.
называется обратной для функции y = f(x) , если область определения функции y является областью изменения функции x.
Графики взаимно обратных функций симметричны относительно биссектрисы первого координатного угла.
Y= x3
x=y3
0 x
Предел функции при x 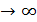
Определение.Число А называется пределом функции y= f(x) при x 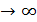 , если каково бы ни было положительное число
, если каково бы ни было положительное число  , можно найти такое число N , что для всех x , больших N , выполняется неравенство
, можно найти такое число N , что для всех x , больших N , выполняется неравенство  Обозначается
Обозначается 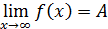 .
.
Коротко это определение можно записать так: число А называется пределом функции y = f(x) при x 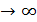 , если
, если 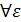 (
( 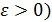
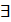 N
N 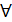 x (x
x (x 
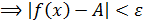 .
.
Раскроем последнее неравенство . –  < f(x) – A <
< f(x) – A <  или (A –
или (A – 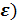 < f(x) <( A +
< f(x) <( A + 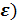 Геометрически это неравенство можно изобразить следующим образом:
Геометрически это неравенство можно изобразить следующим образом:
y
A A+ 
A- 
0 .N x
Определение. Число А называется пределом функции y =f(x) при x 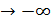 , если
, если 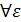 (
( 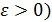
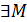
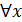 (x <M)
(x <M) 
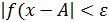 .
.
Изобразим геометрически.
Y A+ 
A
A- 
0 .M x
Предел функции при x 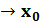
Определение. Число А называется пределом функции y=f(x) при x 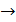 x0 слева, если каково бы ни было положительное число
x0 слева, если каково бы ни было положительное число  , найдётся такое число N ( меньше x0), что для всех x, лежащих между N и x0 (N<x<x0 ) ,выполняется неравенство
, найдётся такое число N ( меньше x0), что для всех x, лежащих между N и x0 (N<x<x0 ) ,выполняется неравенство 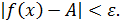 Обозначается:
Обозначается:  .
.
Число А называется пределом функции y = f(x) при x 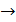 x0 слева , если
x0 слева , если 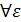 (
( 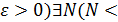 x0 )
x0 ) 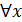 (N<x<x0 )
(N<x<x0 ) 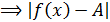 <
<  . Геометрически:
. Геометрически:
Y
A+ 
A
A- 
0 .N x0 x
Определение.Число А называется пределом функции y =f(x) при x 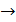 x0 справа , если каково бы ни было положительное число
x0 справа , если каково бы ни было положительное число  найдётся такое число М >x0 , что для всех x ,лежащих между x0 и М ( x0 <x<M) выполняется неравенство
найдётся такое число М >x0 , что для всех x ,лежащих между x0 и М ( x0 <x<M) выполняется неравенство 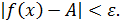 Обозначается
Обозначается 
Число А называется пределом функции y =f(x) при x 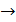 x0 справа , если
x0 справа , если 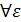 (
(  x0 )
x0 ) 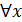 (x0<x<M )
(x0<x<M ) 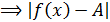 <
<  . Геометрически:
. Геометрически:
y
A+ 
A
A- 
0 x0 .M x
Пределы слева и справа называются односторонними пределами.
Если оба предела равны , то говорят , что функция y(x) в точке x = x0 имеет предел.
Определение. Число А называется пределом функции y = f(x) при x 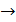 x0, если каково бы ни было
x0, если каково бы ни было  >0, можно найти такие числа M и N ( N<x0 <M) , что для всех x, лежащих в интервале ] N, M [ выполняется неравенство
>0, можно найти такие числа M и N ( N<x0 <M) , что для всех x, лежащих в интервале ] N, M [ выполняется неравенство 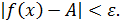
Число А называется пределом функции y = f(x) при x 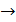 x0 , если
x0 , если 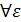 (
( 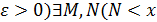 0 <M)
0 <M) 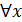 (x
(x 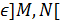 )
) 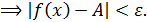 Геометрически:
Геометрически:
y
A+ 
A
A- 
0 .N .x0 .M x
Определение. Любой интервал, содержащий точку x0 называется окрестностью точки x0 .
Пример.Проверить , есть ли предел функции f(x) =  в
в
точке x0 =3.
Решение. Найдём односторонние пределы:  =2 ;
=2 ; 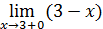 =0. 2
=0. 2 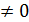 , односторонние пределы не равны, значит в точке x0 =3 функция не имеет предела. Геометрически:
, односторонние пределы не равны, значит в точке x0 =3 функция не имеет предела. Геометрически:
y
0 .3 .4 x
Определение. Функция y=f(x) называется бесконечно малой (б.м) при x 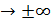 ,при x
,при x 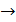 x0, если её предел равен нулю.
x0, если её предел равен нулю.
Определение.Функция y=f(x) называется бесконечно большой (б.б) при x 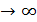 ,при x
,при x 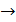 x0 , если для любого положительного числа L можно подобрать такое число N, что для всех значений x>N , выполняется неравенство
x0 , если для любого положительного числа L можно подобрать такое число N, что для всех значений x>N , выполняется неравенство 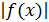 >L.
>L.
Символически это записывается так: 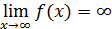 ,
, 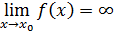
Принято символически обозначать: 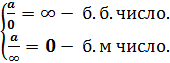
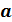 =const.
=const.
Примеры. 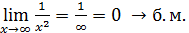 функция;
функция;  = 2
= 2
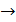 не б.м. функция.
не б.м. функция.
Определение. Функция y=f(x) называется ограниченной на некотором множестве М значений аргумента x, если существует такое число С , что для всех x 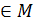 выполняется неравенство
выполняется неравенство 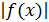 <C.
<C.
Лекция17. Основные теоремы о бесконечно малых функциях и о пределах при x 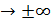 , x
, x 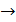 x0 , x
x0 , x 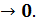
Теорема 1.Если 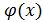 и
и 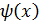 две бесконечно малые функции , то и их
две бесконечно малые функции , то и их 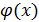
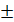
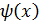 - б.м. функция.
- б.м. функция.
Теорема 2.Произведение б.м. функции на ограниченную является б.м. функцией.
Теорема 3.Произведение 2-х б.м. функций есть функция б.м. ; произведение б.м. функции на число есть функция б.м..
Теорема 4.Если функция y = f(x) является б.б. , то функция 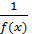 есть б.м. и обратно , если f(x) б.м. , то
есть б.м. и обратно , если f(x) б.м. , то  есть б.б. функция.
есть б.б. функция.
Теорема 5. Если функция имеет предел на некотором интервале , то она ограничена на нём.
Теорема 6. (  Если функция y = f(x) имеет предел , равный А , то её можно представить , как сумму числа А и некоторой б.м. функции , то есть
Если функция y = f(x) имеет предел , равный А , то её можно представить , как сумму числа А и некоторой б.м. функции , то есть 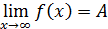 , то f(x) = A +
, то f(x) = A + 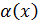 , где
, где 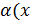 ) – б. м. функция.
) – б. м. функция.
Доказательство. Пусть 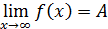 , рассмотрим соотношение f(x) – A =
, рассмотрим соотношение f(x) – A = 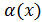 , докажем , что
, докажем , что 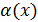 - б.м. функция . Из определения предела следует
- б.м. функция . Из определения предела следует
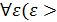 0)
0) 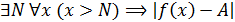 <
<  ,то есть
,то есть 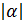 <
<  , так как
, так как  – сколь угодно малое положительное число , то
– сколь угодно малое положительное число , то 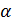 и подавно мало и можно считать его б.м. величиной,ч. т.д..
и подавно мало и можно считать его б.м. величиной,ч. т.д..
Теорема 7. (обратная).Если функцию можно представить ,как сумму числа А и некоторой б.м. функции , то число А является пределом функции f(x).
Свойства пределов
1. Если  im f(x)= A,
im f(x)= A,  im
im 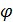 (x ) = B , то
(x ) = B , то  im{ f(x )
im{ f(x ) 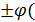 x)} =
x)} =  im f(x)
im f(x) 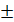
 im
im 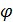 (x ).
(x ).
2. Если 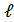 im f(x)= A,
im f(x)= A,  im
im 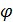 (x ) = B , то
(x ) = B , то  im{ f(x)
im{ f(x) 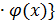 =
=  im f(x)
im f(x) 
 im
im 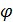 (x ).
(x ).
3. Постоянный множитель можно выносить за знак предела.
 im{k
im{k 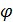 (x )} = k
(x )} = k  im
im 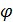 (x ), k – const.
(x ), k – const.
4. Если  im f(x)= A,
im f(x)= A,  im
im 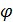 (x ) = B , В
(x ) = B , В 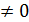 , то
, то  .
.
5. 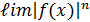 =
= 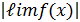 n
n
6. 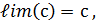 с = сonst.
с = сonst.
Дата добавления: 2016-06-05; просмотров: 1997;











