Лекция 22. Производные некоторых элементарных функций.
1. y = c – const. y
y=c
0  x0
x0  x0+
x0+ 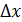 x
x
Из рисунка видно , что  y = 0 , значит
y = 0 , значит 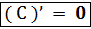
2. y = 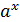 - показательная функция ,
- показательная функция , 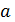 > 0 ;
> 0 ; 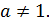
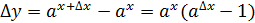 ; (
; ( 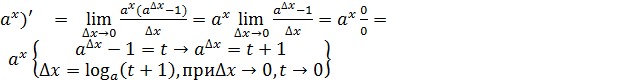 =
= 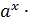
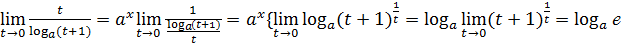 , воспользуемся формулой
, воспользуемся формулой 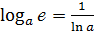 , получим
, получим 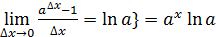 .
.
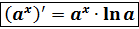 ,если
,если 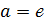 ,то
,то 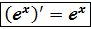
4. y = 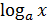 – логарифмическая функция.
– логарифмическая функция.
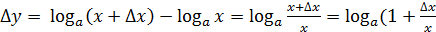 ).
).
( 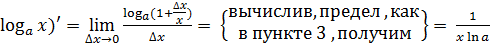 , то есть
, то есть
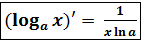 , если
, если  , то
, то 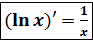
Из школы известно:
5. y = sinx ; 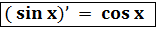 ; 6. y = cos x ;
; 6. y = cos x ; 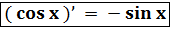
7. y = 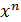 - степенная функция. n- любое действительное число.
- степенная функция. n- любое действительное число. 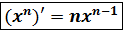
8. y = tg x ; 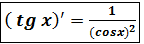
9. y = ctg x ; 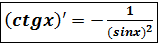
Производная обратной функции
Пусть y = f(x) и x = 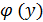 - 2 непрерывные взаимно обратные функции. Пусть известно f ’(x) =
- 2 непрерывные взаимно обратные функции. Пусть известно f ’(x) = 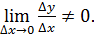 Чтобы найти
Чтобы найти 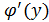 , надо найти
, надо найти 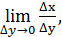 т.к. при
т.к. при 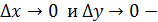 функции непрерывны , то
функции непрерывны , то 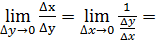
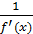 , окончательно
, окончательно 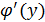 =
= 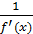 или
или 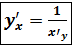
Примеры.
1. y = 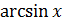 , обратная функция x = sin y в (
, обратная функция x = sin y в ( 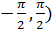 ;
; 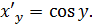
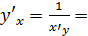
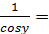
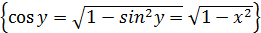 =
= 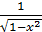 .
. 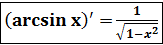
2. Аналогично , 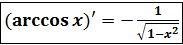 ;
; 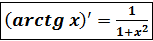 ;
;

Производные гиперболических функций
Определение. Гиперболическим синусом sh x , гиперболическим косинусом сh x , гиперболическим th x , cth x называются функции вида :
Sh x = 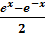 ; ch x =
; ch x = 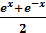 ; th x =
; th x = 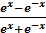 ; cth =
; cth = 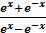
Справедливы соотношения : c 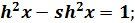 th x=
th x= 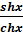 ; cthx =
; cthx = 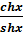 .
.
Y y
y=chx
y=cthx
 1 1
1 1
Y=thx
0 x 0 x
Y=shx -1
График функции y = ch x называется цепной линией.
( sh x)’ = ch x ; (ch x)’ = sh x ; (th x)’ = 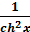 ; ( cth x)’ = -
; ( cth x)’ = - 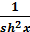 .
.
Доказать самим.
Таблица основных формул дифференцирования
для сложной функции y’x =y’u 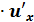 .
.
U = u(x)
1. (С)’ = 0. 11. ( 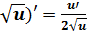 .
.
2. ( 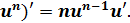 12. (
12. ( 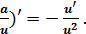
3. ( 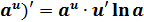 . 13. (arcsin u)’ =
. 13. (arcsin u)’ = 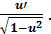
4. ( 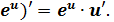 14. (arccos u)’ = -
14. (arccos u)’ = - 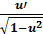 .
.
5. ( 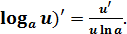 15. (arctg u)’ =
15. (arctg u)’ = 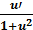 .
.
6. ( 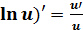 . 16. (arcctg u)’ = -
. 16. (arcctg u)’ = - 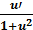 .
.
7. (sin u)’ = cos u 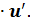 17. (sh u)’ = ch u
17. (sh u)’ = ch u 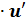 .
.
8. (cos u)’ = - sin u 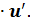 18 . (ch u)’ = sh u
18 . (ch u)’ = sh u 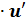 .
.
9. (tg u)’ = 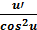 . 19. ( th u)’ =
. 19. ( th u)’ = 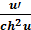 .
.
10. (ctg u)’ =- 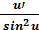 . 20. (cth u)’ = -
. 20. (cth u)’ = - 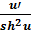 .
.
Примеры.
1. Найти y’ , если y = sin x3.
Решение.Воспользуемся формулой 7 из таблицы : ( sin x3 )’ = cos x3 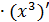 =
=
= cos x3 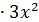 . Ответ:( sin x3 )’ = cos x3
. Ответ:( sin x3 )’ = cos x3 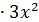 .
.
2. Найти y’ , если y = 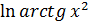 .
.
Решение.Воспользуемся формулой 6 из таблицы: ( 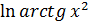 )’ =
)’ = 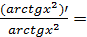
= 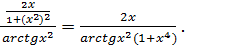 Ответ:(
Ответ:( 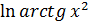 )’ =
)’ = 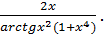
Дата добавления: 2016-06-05; просмотров: 2603;











