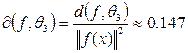Аппроксимация тригонометрическими полиномами кусочно-гладких функций

Функция 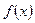 называется кусочно-гладкой на отрезке
называется кусочно-гладкой на отрезке 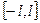 , если этот отрезок можно разбить на конечное число отрезков, в каждом из которых
, если этот отрезок можно разбить на конечное число отрезков, в каждом из которых 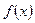 – гладкая функция, т.е.непрерывна вместе со своей первой производной.
– гладкая функция, т.е.непрерывна вместе со своей первой производной.
| Теорема | Тригонометрический ряд Фурье кусочно-гладкой функции 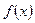 на отрезке на отрезке 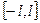 сходится к значению сходится к значению 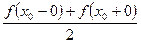 в точке в точке 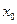 ( сходиться к ( сходиться к  в точках непрерывности функции).
В обеих граничных точках сумма ряда равна среднему арифметическому ее предельных значений в этих точках, т.е. в точках непрерывности функции).
В обеих граничных точках сумма ряда равна среднему арифметическому ее предельных значений в этих точках, т.е. 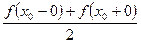
| ||||
| Пример | Найти ряд Фурье для функции
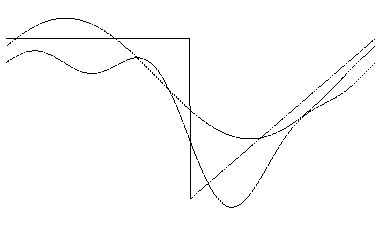
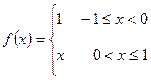 Представить графически приближение этой функции с помощью тригонометрических многочленов степеней
Представить графически приближение этой функции с помощью тригонометрических многочленов степеней 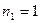 , , 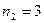 . Оценить погрешность среднеквадратического приближения . Оценить погрешность среднеквадратического приближения 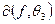 . .
| ||||
| Решение | Определяем коэффициенты Фурье (по формуле (4))
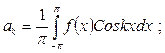 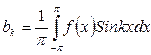 Сделаем замену переменных :
Сделаем замену переменных : 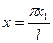 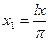 .
Тогда .
Тогда 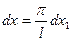 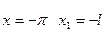
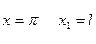 и формулы (3), (4) примут вид:
и формулы (3), (4) примут вид:
Т.е. (3), (4) и (3'), (4') эквивалентны! Считать удобнее по формулам (3'), (4'). Определяем коэффициенты Фурье (у нас
Т.о. ряд Фурье имеет вид
Многочлен наилучшего приближения получаем из последней формулы:
Погрешность приближения находим по формуле:
( следует из
т.к.
|
Дата добавления: 2016-11-04; просмотров: 2779;

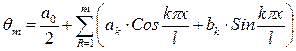
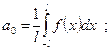
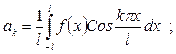
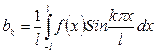
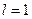 - функция определена на интервале
- функция определена на интервале 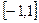 ):
):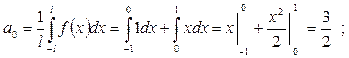
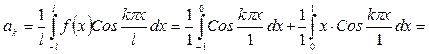
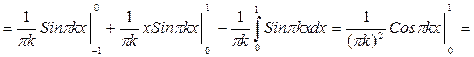
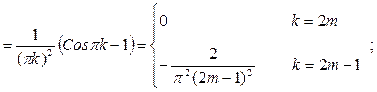
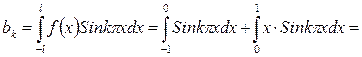
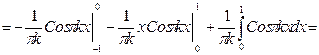
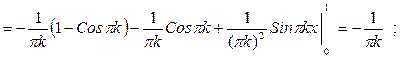
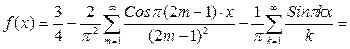
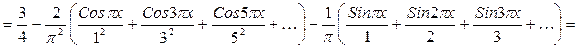
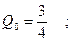
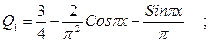
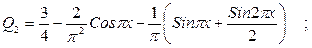
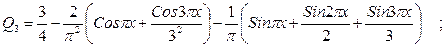
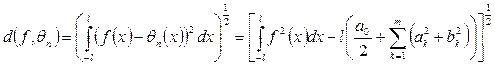
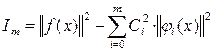 )
)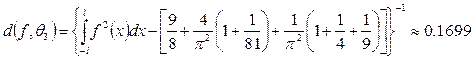
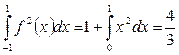 ,
, то
то