Алгоритм оценочных (штрафных) функций
Умело подобранные оценочные функции (в некоторых источниках - штрафные функции) могут значительно сократить полный перебор и привести к решению достаточно быстро в сложных задачах. В нашей задаче о людоедах и миссионерах в качестве самой простой целевой функции при выборе очередного состояния можно взять число людоедов и миссионеров, находящихся "не на месте" по сравнению с их расположением в описании целевого состояния. Например, значение этой функции f=x+y для исходного состояния f0=6, а значение для целевого состояния f1=0.
Эвристические процедуры поиска на графе стремятся к тому, чтобы минимизировать некоторую комбинацию стоимости пути к цели и стоимости поиска. Для задачи о людоедах введем оценочную функцию:
f(n) = d(n) + w(n)где d(n) - глубина вершины n на дереве поиска и w(n) - число находящихся не на нужном месте миссионеров и людоедов. Эвристика заключается в выборе минимального значения f(n). Определяющим в эвристических процедурах является выбор оценочной функции.
Рассмотрим вопрос о сравнительных характеристиках оценочных целевых функций на примере функций для игры в "8" ("пятнашки"). Игра в "8" заключается в нахождении минимального числа перестановок при переходе из исходного состояния в конечное (терминальное, целевое).
| * | ||
| * | ||
Рассмотрим две оценочные функции:
h1(n) & = Q(n)h2(n) & = P(n) + 3S(n),где Q(n) - число фишек не на месте; P(n) - сумма расстояний каждой фишки от места в ее целевой вершине; S(n) - учет последовательности нецентральных фишек (штраф +2 если за фишкой стоит не та, которая должна быть в правильной последовательности; штраф +1 за фишку в центре; штраф 0 в остальных случаях).
Сравнение этих оценочных функций приведено в таблица 3.1.
| Таблица 3.1. Сравнение оценочных функций | ||||
| Оценочная функция h | Стоимость (длина) пути L | Число вершин, открытых при нахождении пути N | Трудоемкость вычислений, необходимых для подсчета h S | Примечания |
| h1 S0S1 | 5>18 | 13100-8!(=40320) | 8 | Поиск в ширину |
| h2 S0S1 | 518 | 1143 | 8*2+8+1+1 | Поиск в глубину |
На основе сравнения этих двух оценочных функций можно сделать выводы.
· Основу алгоритма поиска составляет выбор пути с минимальной оценочной функцией.
· Поиск в ширину, который дает функция h1, гарантирует, что какой-либо путь к цели будет найден. При поиске в ширину вершины раскрываются в том же порядке, в котором они порождаются.
· Поиск в глубину управляется эвристической компонентой 3S(n) в функции h2 и при удачном выборе оценочной функции позволяет найти решение по кратчайшему пути (по минимальному числу раскрываемых вершин). Поиск в глубину тем и характеризуется, что в нем первой раскрывается та вершина, которая была построена самой последней.
· Эффективность поиска возрастает, если при небольших глубинах он направляется в основном в глубь эвристической компонентой, а при возрастании глубины он больше похож на поиск вширь, чтобы гарантировать, что какой-либо путь к цели будет найден. Эффективность поиска можно определить как E=K/L*N*S, где K и S (трудоемкость) - зависят от оценочной функции, L - длина пути, N - число вершин, открытых при нахождении пути. Если договориться, что для оптимального пути E=1, то K=L0*N0*S0.
Алгоритм минимакса
В 1945 году Оскар Моргенштерн и Джон фон Нейман предложили метод минимакса, нашедший широкое применение в теории игр. Предположим, что противник использует оценочную функцию (ОФ), совпадающую с нашей ОФ. Выбор хода с нашей стороны определяется максимальным значением ОФ для текущей позиции. Противник стремится сделать ход, который минимизирует ОФ. Поэтому этот метод и получил название минимакса. На рис. 3.5 приведен пример анализа дерева ходов с помощью метода минимакса (выбранный путь решения отмечен жирной линией).
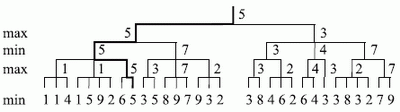
Рис. 3.5.Дерево ходов
Развивая метод минимакса, назначим вероятности для выполняемых действий в задаче о миссионерах и людоедах:
P([2 : 0]R) = 0; 8; P([1 : 1]R) = 0; 5;P([0 : 2]R) = 0; 9;P([1 : 0]R) = 0; 3; P([0 : 1]R) = 0; 3:Интуитивно понятно, что посылать одного людоеда или одного миссионера менее эффективно, чем двух человек, особенно на начальных этапах. На каждом уровне мы будем выбирать состояние по критерию Pi. Даже такой простой подход позволит нам избежать части тупиковых состояний в процессе поиска и сократить время по сравнению с полным перебором. Кстати, этот подход достаточно распространен в экспертных продукционных системах.
Дата добавления: 2018-05-10; просмотров: 1718;











